Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
ГМТ с постоянным углом
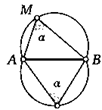
Теорема. Геометрическим местом точек М, из которых данный отрезок АВ виден под постоянным углом а, является объединение двух дуг окружностей с концами в точках А и В.
1. Дан отрезок АВ и угол а. Постройте все такие точки М, что IAMB = а.
2. Дан отрезок АВ. Где находятся все такие точки М, что ZAMB> 90°?
3. На сторонах выпуклого четырехугольника как на диаметрах построили круги. Покроют ли они весь четырехугольник?
4. а) На сторонах выпуклого пятиугольника как на диаметрах построили круги. Может ли существовать точка, покрытая всеми этими кругами? б) Тот же вопрос для невыпуклого пятиугольника.
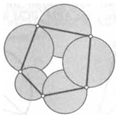
5. Противоположные углы четырехугольника тупые. Докажите, что соединяющая их диагональ меньше другой его диагонали.
6. Из некоторой точки внутри квадрата две его противоположные стороны видны под прямыми углами. Докажите, что данная точка — центр квадрата.
7. Найдите геометрическое место середин хорд данной окружности, проходящих через данную точку.
8. На плоскости даны отрезок АВ и некоторая точка О. Через точку О проводят произвольные прямые. Из любой точки отрезка АВ на каждую из таких прямых опускают перпендикуляр. Что представляет собой множество оснований этих перпендикуляров?
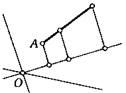
*9. На плоскости даны четыре точки. Найдите множество центров прямоугольников, образуемых четырьмя прямыми, проходящими соответственно через данные точки.
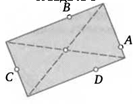
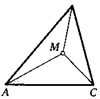
10. Дан треугольник. Постройте точку так, чтобы каждая его сторона была видна из этой точки под одним и тем же углом. Для любого ли треугольника есть такая точка?
11. (Точки Брокара.) Существуют ли внутри треугольника АВС такие точки М, что углы ABM, ВСМ и САМ равны? Сколько таких точек?
В
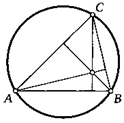
12. На окружности заданы точки А и В. Точка С движется по окружности. Найдите геометрическое место точек пересечения: а) высот; б) биссектрис треугольников АВС.
13. Постройте треугольник по стороне, противоположному углу и высоте, проведенной из этого угла.
14. Постройте треугольник по стороне, противоположному углу и медиане, проведенной к этой стороне. Может ли задача иметь более двух решений?
15. Постройте параллелограмм по длинам его сторон и углу между диагоналями.
16. Постройте треугольник по стороне, противоположному углу и радиусу вписанной в него окружности.
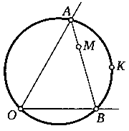
17. Внутри угла с вершиной О даны точки М и К, Через точки О и К проведите окружность так, чтобы она пересекала стороны угла в точках А и В, причем точка М лежала бы на отрезке А£.
*18. Постройте треугольник по его основанию, противоположному углу и медиане, проведенной к боковой стороне. Сколько решений может иметь задача?