Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Аксиомы прямой
Аксиомы ПРЯМОЙ
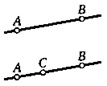
точка С лежит между А и В
А
отрезок АВ
![]()
луч АВ
1. Для любой прямой на плоскости всегда можно взять точку, лежащую на ней, и точку, не лежащую на этой прямой.
2. Через любые две точки на плоскости проходит только одна прямая.
3. Из любых трех точек на прямой только одна лежит между двумя другими.
4. Прямая всегда разбивает плоскость на две части (полуплоскости)1. Если концы отрезка лежат в разных полуплоскостях, то он пересекает прямую; если же его концы принадлежат одной полуплоскости, то он ее не пересекает.
Отрезком называется множество всех точек на прямой, лежащих между двумя данными ее точками. Данные точки называются концами отрезка. Концы отрезка также принадлежат ему.
Лучом называется множество всех точек на прямой, лежащих по одну сторону от данной ее точки2. Данная точка называется началом луча. Начало луча также принадлежит ему.
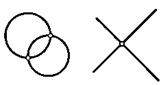
1. Как видно из рисунка, две окружности могут пересекаться в двух точках. Докажите, что две различные прямые могут пересекаться только в одной точке.
2. Через точку на плоскости провели прямую. Докажите, что через данную точку можно провести еще одну прямую, отличную от первой.
3. Сколько существует лучей с началом в данной точке А, проходящих через данную точку В?
4. На прямой отметили три точки. Сколько всего получилось лучей с началами в данных точках?
5. На плоскости отметили четыре точки. Через любые две из них провели прямую. Сколько всего при этом могло получиться прямых? (Разберите все случаи.)
6. Нарисуйте четыре прямые так, чтобы они пересекали друг друга ровно в пяти точках.
7. Могут ли семь прямых пересекаться ровно в девяти точках?
8. В каком наибольшем числе точек могут пересекаться 20 прямых?
9. В каком числе точек пересекают друг друга 15 прямых, никакие три из которых не пересекаются в одной точке, если среди них есть ровно две параллельные?
10. В каком числе точек пересекаются 10 прямых, если среди них нет параллельных и ровно три из них проходят через одну точку?
11. Незнайка утверждает, что окружность — это прямая. Почему он не прав? Приведите три возражения, ссылаясь на приведенную таблицу и аксиомы.
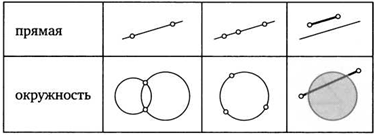
12. Отрезки АВ, ВС и СЕ пересекаются с данной прямой, а их концы не лежат на ней. Что можно сказать об отрезке АЕ?
13. Точка А лежит на прямой, отрезок ВС пересекает прямую. Пусть М — произвольная точка на отрезке АВ. Докажите, что отрезок СМ пересечет прямую.
14. Фома утверждает, что точки на прямой принадлежат сразу двум полуплоскостям, границей которых является данная прямая. Какая аксиома тогда нарушается и почему?
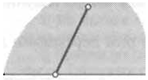
15. (Теорема.) Прямая пересекает одну сторону треугольника в точке, отличной от вершины. Докажите, что она пересечет еще одну его сторону.
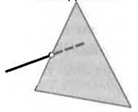
16. Нарисуйте пятиугольную звезду. Проведите прямую, пересекающую все ее пять звеньев. Можно ли провести эту прямую так, чтобы она не проходила через вершины звезды? Ответ поясните.
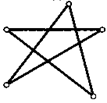
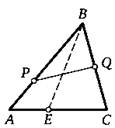
17. На сторонах АВ и ВС треугольника АВС взяли точки Р и Q, а на стороне АС — точку Е. Докажите, что отрезок BE пересекает прямую PQ.
18. Десять точек на плоскости попарно соединили отрезками. Прямая не проходит ни через одну из точек. Может ли она пересечь ровно 20 отрезков?
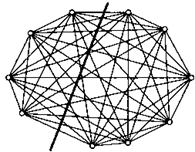
19. На плоскости отметили несколько точек и попарно соединили их все отрезками. Прямая не проходит ни через одну из точек. Оказалось, что она пересекла ровно 21 отрезок. Сколько отрезков не пересекла прямая? Внимание: у задачи может быть несколько решений!
20. Немецкий математик Клейн утверждал, что «плоскость» — это внутренность некоторого круга, а «прямые» на ней — отрезки с концами на окружности. Проверьте, что все пройденные нами аксиомы на такой «плоскости» выполняются. Как будет на ней выглядеть луч?