Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016

Внешний угол треугольника

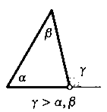
Внешим углом треугольника называют угол, смежный одному из углов треугольника. Всего у треугольника есть шесть внешних углов.

Теорема о внешнем угле. Внешний угол треугольника больше любого угла треугольника, не смежного с ним.

1. Используя приведенный чертеж, докажите теорему о внешнем угле. Как изменить показанное на этом чертеже построение для доказательства того, что данный внешний угол треугольника больше угла ВАС?

2. Могут ли в треугольнике быть два прямых угла? А два тупых?

3. Докажите, что сумма любых двух углов треугольника меньше 180°.

4. К данной прямой проведены два перпендикуляра. Докажите, что они не могут пересекаться.

5. В треугольнике АВС взята произвольная точка О. Докажите, что ZAOC > ZABC.

6. На сторонах АВ и ВС треугольника АВС взяли произвольные точки М и К, причем отрезки АК и СМ пересекаются в точке О. Докажите, что ZAMC 4- ZAKC > ZAOC.