Поурочные разработки по Математике 6 класс
Пропорции - урок 4 - ОТНОШЕНИЯ И ПРОПОРЦИИ - ОБЫКНОВЕННЫЕ ДРОБИ
Цели: формировать навык нахождения неизвестных членов пропорции, решения уравнений, имеющих вид пропорции; воспитывать умение оценивать объективно труд своих товарищей; проверить знания и умения учащихся по изученному материалу.
Ход урока
I. Организационный момент
II. Устный счет
1. Выразите неизвестные переменные а, b, с, d: а : b = с : d.
2. Найдите значение выражений: 
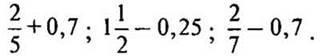
— Подумайте, в каких дробях удобнее считать. (В обыкновенных. )
3. Из следующих равенств составьте пропорцию: 15 · 4 = 12 · 5; 12 · 3 = 9 · 4.
4. Сколько концов у трех с половиной палок? (8.)
5. Какое число делится на все числа без остатка? (0.)
6. Как по-другому можно сформулировать этот вопрос? (Какое число кратно всем числам?)
III. Индивидуальная работа
1 карточка
1. Заполните * числами, чтобы пропорции были верными:
13 : 18 = 26 : *;
15 : 24 = * : 72.
2. Даны три целых числа: 2, 6 и 8. Используя только этот набор чисел, замените * в записях для получения верных пропорций:
а) 3 : * = * : 4;
б) * : 12 = 4 : *.
2 карточка
1. Заполните * числами, чтобы пропорции были верными:
13 : * = 26 : 54;
* : 36 = 48 : 72.
2. Даны три целых числа: 2, 6 и 8. Используя только этот набор чисел, замените * в записях для получения верных пропорций:
а) 5 : 15 = * : *;
б) * : * = 25 : 100.
Задания сдаются на проверку сильным учащимся.
IV. Сообщение темы урока
— Сегодня на уроке продолжим работу над темой «Пропорция».
V. Закрепление изученного материала
1. № 764 (в) стр. 125 (самостоятельно).
(Ответ:
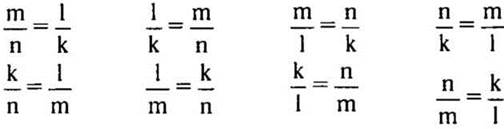 )
)
2. № 762 (г, д) стр. 125 (самостоятельно).
— Объясните, что значит верная пропорция.
г) 0,35 · 0,18 = 0,063; 0,6 · 0,106 = 0,0636.
д) 18 · 5 = 90; 30 · 3 = 90.
(Ответы: г) верна; д) верна.)
VI. Физкультминутка
VII. Работа над задачей
1. № 730 стр. 119 (после разбора самостоятельно, проверка — устное проговаривание решения).
— Прочитайте задачу.
— Как узнать, какую часть дороги построил второй город? (Из целого, или единицы, вычесть ту часть дороги, что построил первый город.)
— Как узнать, во сколько раз часть дороги, построенная первым городом, больше, чем часть дороги, построенная вторым? (Большее число разделить на меньшее.)
Решение:
Пусть 1 — вся дорога.
1)  (дороги) — построил второй город.
(дороги) — построил второй город.
2) 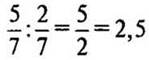 (раза).
(раза).
(Ответ: 2,5 раза.)
2. № 738 (а) стр. 120 (самостоятельно, взаимопроверка).
— Сколько углов в треугольнике?
— Зная, что сумма углов треугольника равна 180°, и зная градусную меру двух углов, что можно найти?
— Решите задачу самостоятельно.
3. Индивидуальная работа.
— Подойдите к доске, кто не знает, как решать задачу.
Решение:
180 — 75 — 80 = 25° — градусная мера угла А.
— Кто решил по-другому?
Решение:
180 — (75 + 80) = 25° — градусная мера угла А.
VIII. Повторение изученного материала
№ 767 стр. 126 (устно).
Решение:
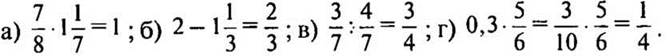
IX. Самостоятельная работа (10—15 мин)
Вариант I
1. Выразите неизвестные переменные а, b, с, d: d : b = а : с.
2. Выразите неизвестные переменные к, s, n, f: 
3. Решите уравнение: 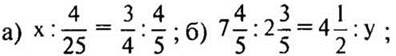 в) 15,04 : 2,688 = х : 26,88.
в) 15,04 : 2,688 = х : 26,88.
Вариант II
1. Выразите неизвестные переменные а, b, с, m: с : а = b : m.
2. Выразите неизвестные переменные с, у, n, р: 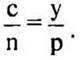
3. Решите уравнение: 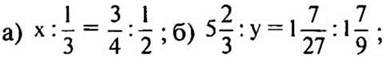 в) 15,48 : 64,8 = 55,9 : х.
в) 15,48 : 64,8 = 55,9 : х.
X. Подведение итогов урока
— Останется ли пропорция верной, если поменять местами какой-нибудь средний ее член с одним из крайних?
— Приведите пример.
— Останется ли пропорция верной, если оба средних члена поменять местами с крайними членами?
— Ответ обоснуйте на своем примере.
Домашнее задание
№ 775, 781 (б), 777 (г) стр. 127.