Математика 5 класс - Поурочные разработки
Признаки делимости на 2, на 5, на 10 - Признаки делимости - Делимость чисел
Цели: ввести новый математический термин «признак делимости», познакомить учащихся с признаками делимости на 2, на 5, на 10.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите, выполнив вычисления по схеме (рис. 124).
2. Не выполняя вычисления, определите, делится ли значение выражения:
а) 35 + 120 на 5; б) 49 · 27 на 7; в) 49 + 63 на 7; г) 32 - 15 на 4; д) 42 · 15 на 6. Ответ объясните.
3. У, № 568.
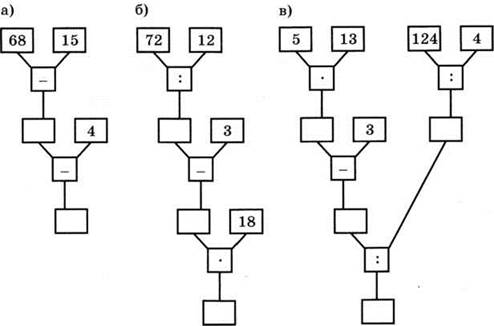
Рис. 124
III. Изучение нового материала.
1. Признак делимости на 2.
Представьте, что сказочный волшебник отправился «в поход» по натуральному ряду чисел. Сделав первый шаг, он наступил левой ногой на число 1, вторым шагом наступил правой ногой на число 2. Затем левой — на 3, правой — на 4. Какой ряд пройдет правая нога волшебника? Представить это нетрудно: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ... . Это ряд четных чисел, или ряд чисел, кратных 2. Как узнать, принадлежит ли этому ряду число 2753, т. е. делится на 2 или нет? Обратим внимание на последние цифры этих чисел: 2, 4, 6, 8, 0, 2, 4, 6, 8, 0, 2. Какой вывод можно сделать?
Вывод. Если натуральное число оканчивается одной из цифр 2, 4, 6, 8, 0, то оно четно, т. е. делится на 2, а если оканчивается одной из цифр 1, 3, 5, 7, 9, то оно нечетно, т. е. не делится на 2.
Это правило называется признаком делимости. Признак — правило, пользуясь которым можно легко и удобно обнаружить свойство.
2. Свойства суммы, разности, произведения и частного четных и нечетных чисел. Работа в группах.
1). В следующих таблицах заполните пустые клетки и рядом с каждым четным числом поставьте букву «ч», а рядом с нечетным — букву «н».
а)
Слагаемое |
Слагаемое |
Сумма |
145 н |
236 ч |
381 н |
1024 |
316 |
|
4560 |
7217 |
|
619 |
1148 |
|
157 |
231 |
б)
Уменьшаемое |
Вычитаемое |
Разность |
769 н |
616 ч |
153 н |
3022 |
2984 |
|
9762 |
5499 |
|
7121 |
456 |
|
4893 |
1257 |
в)
Множитель |
Множитель |
Произведение |
91 н |
11 н |
1001 н |
23 |
46 |
|
74 |
22 |
|
153 |
21 |
|
314 |
25 |
г)
Делимое |
Делитель |
Частное |
1024 ч |
64 ч |
16 ч |
315 |
15 |
|
9638 |
79 |
|
10404 |
102 |
|
1353 |
123 |
2). Какие выводы можно сделать? У, № 619, 620, 621.
3. Признаки делимости на 5 и на 10.
1). Запишите ряд чисел, кратных 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, ... .
2). Что заметили в записи этих чисел?
3). Сформулируйте признак делимости на 5.
4). Аналогично сформулируйте признак делимости на 10.
IV. Формирование умений и навыков.
1. Из чисел 147, 285, 612, 140, 95, 78, 2156, 3100, 2005, 6420, 3134 выпишите числа, которые делятся на 2, на 5, на 10.

Какие числа попали в третий столбик? Сделайте вывод. (Те, которые делятся на 5 и на 2.)
2. У, № 571, № 582 (а).
3. Сколько трехзначных чисел, делящихся на 5, можно записать с помощью цифр 0, 2, 7, 5?
4. У, № 593 (а, б).
5. Дополнительно задания по вариантам.
Вариант 1
1. Напишите ряд чисел, кратных 100. Обратите внимание на две последние цифры чисел этого ряда. Сформулируйте признак делимости на 100.
2. Сформулируйте признак делимости на 4.
Вариант 2
1. Напишите ряд чисел, кратных 25. Обратите внимание на две последние цифры чисел этого ряда. Сформулируйте признак делимости на 25.
2. Сформулируйте признак делимости на 4.
V. Итоги урока.
1. Какими цифрами могут оканчиваться четные числа?
2. Какими цифрами могут оканчиваться нечетные числа?
3. Как, не выполняя деления, определить, делится ли данное число на 5?
4. Как, не выполняя деления, определить, делится ли данное число на 10?
5. Какой цифрой оканчивается четное число, которое делится на 5?
6. Может ли нечетное число делиться на четное? Ответ объясните.
VI. Домашнее задание.
У, с. 120, выучить признаки, № 569, 570, 617.