Математика 5 класс - Поурочные разработки
Делители числа. Наибольший общий делитель - Делители и кратные - Делимость чисел
Цель: познакомить учащихся с простейшими понятиями, связанными с понятием делимости чисел (делитель, общий делитель, наибольший общий делитель).
Ход урока
I. Организационный момент.
II. Устная работа.
Вычислите:

III. Актуализация знаний.
1. Рассмотрите схемы (рис. 116). На какой цветок они похожи? Дайте математическое описание «ромашек». Обратите внимание на числа, расположенные на противоположных лепестках. Какая связь между ними и числом в центре?
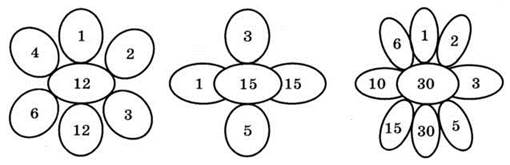
Рис. 116
2. Постройте «ромашки» для чисел 14, 18, 20, 24, 32, 45.
3. Отметьте те «ромашки», которые содержат меньше (больше) всего лепестков. С каким математическим свойством чисел это связано?
4. Найдите числа, для которых «ромашки» состоят из двух, трех, четырех лепестков.
IV. Изучение нового материала.
1. Понятие делителя.
Мы знаем, что, например, число 27 делится на 3. Но почему это утверждение верно? На этот вопрос обычно отвечают так: 27 предметов можно разделить на 3 равные группы по 9 предметов в каждой, и ничего не останется. Примеры: конфеты разложить в три кучки; учеников в классе разделить на три группы. Другими словами, для доказательства этого утверждения к числу 3 надо указать «второй сомножитель» — в данном случае 9, таким образом, чтобы при умножении его на 3 получилось 27. Действительно, 9 · 3 = 27. С другой стороны, 27 не делится на 4, потому что нельзя подобрать такой сомножитель, чтобы 4 · * = 27. Эти рассуждения иллюстрируют уже знакомое нам определение делимости. Число а делится на число b, если существует такое число с, что выполняется равенство а = b · с.
Далее согласно п. 6.1 учебника вводится понятие делителя, показываются разные приемы нахождения всех делителей данного числа, наибольшего общего делителя.
2. Обсуждение изучаемых понятий с учащимися.
1). Может ли делитель числа быть больше самого этого числа? Почему?
2). Докажите, что любое число является делителем самого себя.
3). Какое число является делителем всех чисел?
V. Формирование умений и навыков.
1. Устная фронтальная работа по закреплению нового понятия.
1). Из чисел 1, 2, 3, 4, 5, 6, 7, 12, 30 выберите те, которые являются делителями числа: 12; 30; 35; 45; 120; 140.
2). Назовите по порядку, начиная с наименьшего, все делители числа: 8; 36; 21; 48.
Образец записи: Д (8) = {1; 2; 4; 8}.
3). Как найти все делители данного числа? Можно ли упростить перебор, если вспомнить о парных делителях?
4). Представьте в виде произведения двух множителей всеми возможными способами числа 14, 46, 34, 100. Обратитесь к модели «математическая ромашка». Назовите делители данных чисел.
2. Письменная работа учащихся на доске.
1). У, № 518. Выпишите все делители числа.
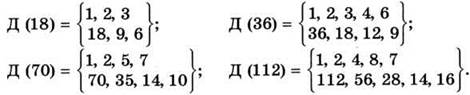
2. Пользуясь результатами предыдущего задания, найдите все общие делители для указанных чисел: а) 36 и 112; б) 112 и 70.
Д (36, 112) = {1, 2, 4}; Д (112, 70) = {1, 2, 7, 14}.
VI. Изучение нового материала.
1. Ввести понятие наибольшего общего делителя.
Образец записи: НОД (36, 112) = 4; НОД (70, 112) = 14.
2. Самостоятельная работа.
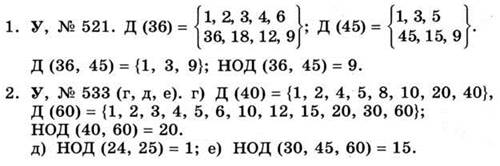
Физкультминутка «Истинно — ложно»
Если утверждение верно, то дети хлопают; если ложно, то дети топают.
• Число 36 имеет 9 делителей.
• Число 15 является делителем 36.
• Число 15 является делителем 45.
• Число 45 имеет 6 делителей.
• Число 3 является наибольшим общим делителем чисел 36 и 45.
• Число 9 является наибольшим общим делителем чисел 36 и 45.
• Числа 40 и 60 делятся на 5.
• Число 15 является делителем 40.
• Число 10 является наибольшим общим делителем чисел 40 и 60.
• Число 20 является наибольшим общим делителем чисел 40 и 60.
• Числа 24 и 25 общего делителя не имеют.
• Наибольший общий делитель чисел 24 и 25 — это 1.
• Наибольший общий делитель чисел 30, 45 и 60 — это 5.
• Наибольший общий делитель этих чисел — это 15.
3. Использование делимости чисел при решении задач. Создание математической модели. Обсуждение задач № 520, 529 из учебника.
VII. Итоги урока.
1. Какое число называется делителем данного натурального числа?
2. Что такое общий делитель двух чисел?
3. Что такое наибольший общий делитель двух чисел?
VIII. Домашнее задание.
У, п. 6.1, № 514, 517, 530, 533 (а, б, в).