Путешествие в историю математики - Свечников А. А. 1995
«Считающие» чертежи
Изображение чисел отрезками во многих случаях помогает не только при решении задач, но и при сложных вычислениях, облегчая умственный труд человека. Рассмотрим пример, в котором чертеж позволяет найти приблизительный ответ без вычислений. Во многих задачах довольно часто скорость движения одного предмета задана километрами в час, а для другого предмета скорость выражена метрами в минуту. При решении таких задач одну из скоростей нужно определить в других единицах измерения. Для выражения скорости в одних и тех же измерениях сделаем чертеж. Проведем прямую, отложим на ней равные отрезки, проставим над их концами числа 1,2, 3..., которые будут выражать скорость в километрах в час.

Затем измерением найдем значение отрезка скорости в 5 м/мин и нанесем на прямую метки, соответствующие отрезкам 5, 10, 15, 20... метров в минуту (см. с. 146).
Теперь у нас получился «считающий» чертеж, который позволит выразить заданное число километров в час в метрах за минуту, и наоборот. Например:

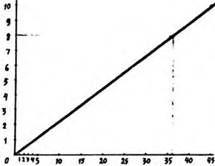
Еще пример. Представьте себя на месте учетчика, который определяет выполнение нормы выработки при вспашке земли. Пусть, например, по плану для трактористов установлена норма выработки ![]() пашни в день. Чтобы легче было подсчитывать, сколько норм выполнил тракторист или целая бригада, сделаем чертеж. На листе клетчатой бумаги (лучше взять миллиметровку) проведем из одной точки две прямые (оси) под прямым углом друг к другу. На горизонтальной оси откладываем равные отрезки и против точек, ограничивающих отрезки, запишем числа 0, 1, 2, 3... На вертикальной оси сделаем то же. Для нашего чертежа против числа 45, стоящего на горизонтальной оси, отсчитаем десять делений вверх и поставим точку. Делаем это так потому, что десять норм выработки составляют 45 га. Указанную точку соединим наклонной прямой с начальной точкой отсчета — точкой пересечения осей, у которой стоит 0.
пашни в день. Чтобы легче было подсчитывать, сколько норм выполнил тракторист или целая бригада, сделаем чертеж. На листе клетчатой бумаги (лучше взять миллиметровку) проведем из одной точки две прямые (оси) под прямым углом друг к другу. На горизонтальной оси откладываем равные отрезки и против точек, ограничивающих отрезки, запишем числа 0, 1, 2, 3... На вертикальной оси сделаем то же. Для нашего чертежа против числа 45, стоящего на горизонтальной оси, отсчитаем десять делений вверх и поставим точку. Делаем это так потому, что десять норм выработки составляют 45 га. Указанную точку соединим наклонной прямой с начальной точкой отсчета — точкой пересечения осей, у которой стоит 0.
Если бригада трактористов вспахала 36 га, то учетчик должен на горизонтальной оси найти число 36 и подсчитать, на какой высоте, выраженной в масштабных единицах, над этой точкой проходит наклонная прямая. В этом месте она отстоит на 8 единиц от горизонтальной оси. Значит, бригада выполнила 8 норм.

Такие чертежи называют номограммами. Номограмма — слово греческое. В переводе оно означает «черчение закона», или «черчение правила», т. е. изображение закона, или правила, чертежом. Номограммы можно применять во многих случаях вычислений.
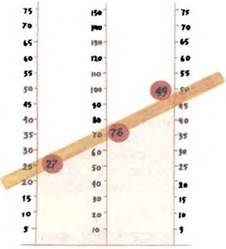
Например, когда требуется часто складывать двузначные числа, можно построить следующую номограмму. Проведем на равных расстояниях одна от другой три прямых под углом к четвертой прямой. На крайних прямых отложим равные масштабные единицы. А на средней прямой такие единицы отложим в два раза мельче. Против делений проставим соответствующие числа. Если потребуется сложить, например, 27 и 49, приложим линейку так, чтобы на левой шкале она проходила через деление 27, а на правой — через деление 49. Ответ 76 можно прочитать на средней шкале. Этой номограммой можно воспользоваться и при вычитании двузначных чисел.
Определение нормы выработки с помощью номограммы.
Сложение двузначных чисел по номограмме.
Подобные «считающие» чертежи, или номограммы, имеют длинную историю. Уже солнечные часы представляли собой «считающий» чертеж на песке, где роль линии выполняла тень от стержня, воткнутого в землю. Греческие математики Евклид, Аполлоний Пергский и другие выражали числа отрезками. Галилей доказывал открытый им закон ускоренного движения тел с помощью построения своеобразной номограммы. Но в то время этого названия не существовало, да и специальным изучением чертежей для вычислительных целей не занимались. Большой вклад в обоснование графического выражения величин внесли математики Ферма, Декарт и Эйлер.
Значительный интерес к разработке правил построения и применения номограмм при вычислениях у математиков появился в XIX в. Первым занялся прямолинейными номограммами в 1843 г. французский математик Л. Лалан. В России изучением метода номограмм занялись лишь в начале XX в. — Н. М. Герсованов (1879 — 1950) и особенно Н. А. Глаголев (1888 — 1945).
Абак. Это, пожалуй, первый вычислительный прибор. Появился он около 2500 лет назад и был широко распространен в Египте, Китае, Греции.
