Высшая математика мини-справочник для ВУЗов
Повторные независимые испытания - ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Ряд испытаний будем называть независимыми по отношению к событию А, если вероятность наступления А в каждом испытании не зависит от результатов прочих испытаний.
Например, выпадение «шестерки» при бросании игральной кости. Вероятность выпадение «шестерки» при каждом бросании не зависит от того, сколько раз она выпадала в других испытаниях.
Пусть проводится n испытаний, в каждом из которых событие А может произойти с одной и той же вероятностью р. Тогда вероятность Рn(m) того, что в серии из п испытаний событие А произойдет ровно m раз (0 ≤ m ≤ n), определяется формулой
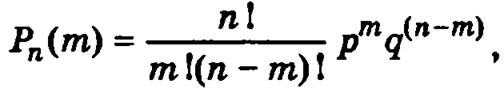
где q = 1 - р, n! = 1 ∙ 2 ∙ 3 ∙...∙ n.
Наиболее вероятное число появлений события А в серии из n испытаний m0 удовлетворяет соотношению
nр - q ≤ m0 ≤ nр + р.
При больших значениях п вероятность Pn(m) приближенно определяется по формуле (локальная теорема Лапласа)
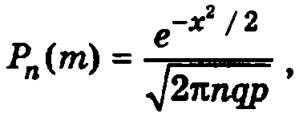
где 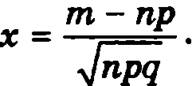
Если вероятность р наступления события А в каждом испытании достаточно мала, а п велико (рn < 10), то
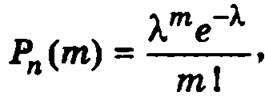
где λ = nр (формула Пуассона).
Вероятность того, что в серии из п испытаний число m наступлений события А окажется заключенным в границах от m1 до m2 для достаточно больших л, находится по формуле (интегральная теорема Лапласа)
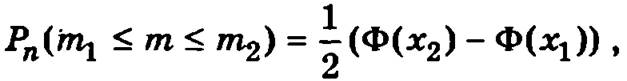
где 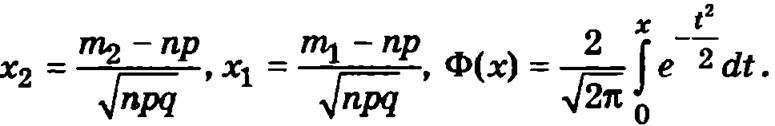
Свойства функции Ф(х):
1. Функция Ф(х) нечетная, то есть
Ф(-x) = -Ф(x).
2. Функция Ф(x) монотонно возрастающая, если x2 > x1, то Ф(х2) > Ф(x1).
3. Для достаточно больших х (х > 5) можно считать Ф(x) ≈ 1.