Степенные ряды - РЯДЫ

Частным случаем функциональных рядов являются степенные ряды, которые в общем случае имеют вид

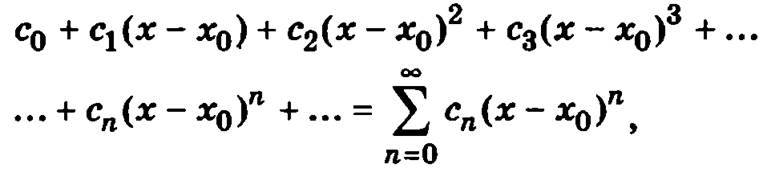
где с0, c1, с2, с3 ,..., сn — числа, именуемые коэффициентами ряда, х0 — некоторое фиксированное значение переменной х.

Чаще имеют дело со степенными рядами в более простой форме:

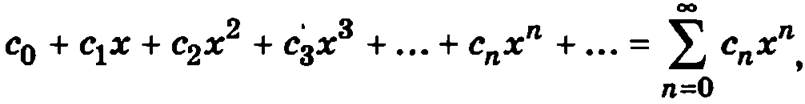
к которой можно прийти, если ввести новую переменную, обозначив через нее выражение х - х0. Далее будем иметь в виду такую форму степенного ряда.

Теорема Абеля

Если степенной ряд сходится при х = х0, то он будет сходиться и притом абсолютно для всех х, для которых |х| < |x0|. Если степенной ряд расходится при х = x0, то он будет расходиться и для всех ху для которых |x| > |x0|.

Интервалом сходимости степенного ряда является интервал, симметричный относительно точки х = 0, вида (-R, R). Величина R называется радиусом сходимости степенного ряда и определяется формулой

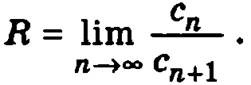
Внутри интервала сходимости (-R, R) степенной ряд сходится, а на концах интервала в точках х = -R и х = R ряд может как сходиться, так и расходиться.

Поэтому при определении области сходимости степенного ряда сходимость его на концах интервала сходимости исследуется отдельно.

Пример. Определим область сходимости степенного ряда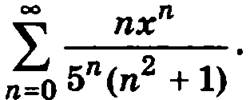

Найдем радиус сходимости данного ряда:

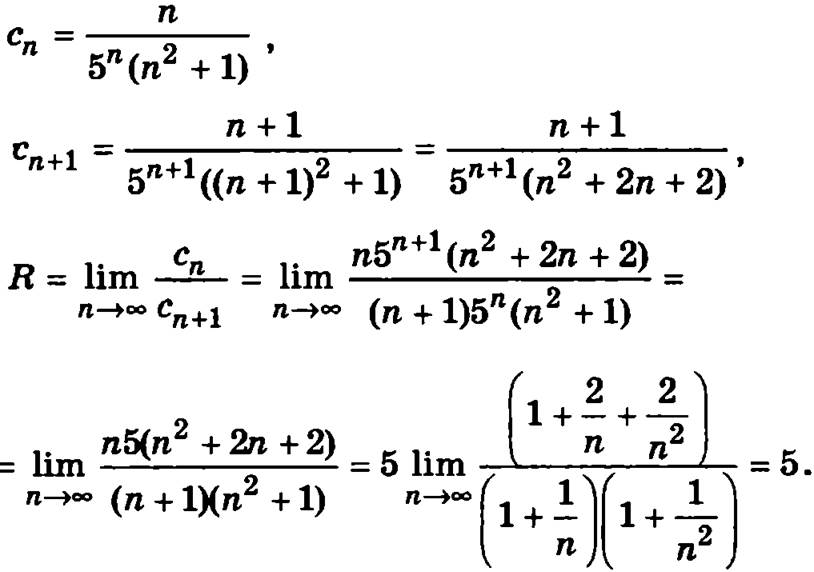
Следовательно, интервал сходимости данного ряда (-5, 5). Исследуем поведение ряда на концах интервала сходимости. Подставим в степенной ряд вместо х значение, соответствующее левой граничной точки интервала сходимости х = -5, получим знакочередующийся ряд:

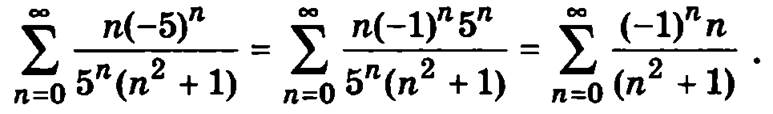
Для исследования сходимости этого ряда используем признак сходимости Лейбница:

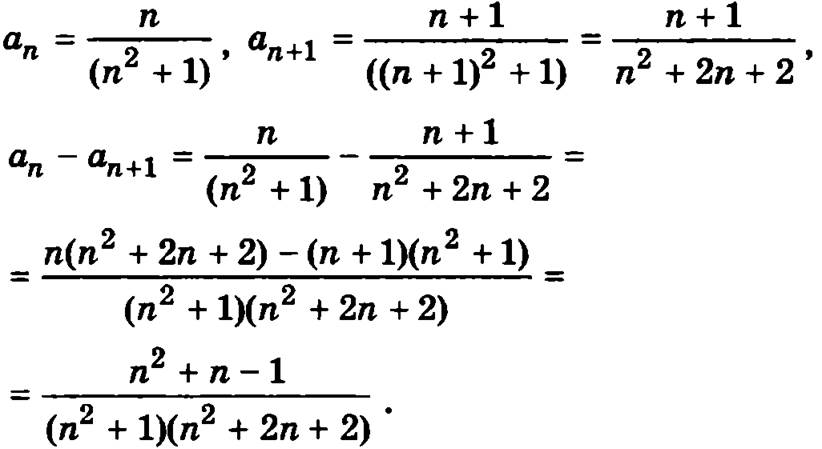
Знаменатель полученной дроби положительный, так как представляет собой произведение положительных величин (n2 + 1) и (n2 + 2n + 2). Числитель дроби n2 + n - 1 положителен приn > 0, и значит, данная дробь будет положительной при n > 0. Следовательно первое условие признака Лейбница аn > аn+1 выполняется при n > 0.

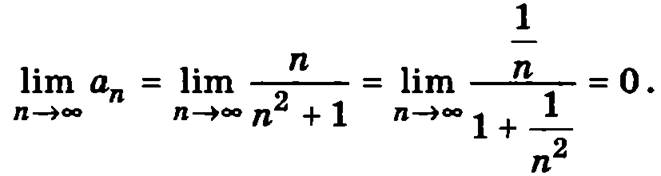
Это означает, что и второе условие признака Лейбница тоже выполняется. Данный ряд сходится, и точку х = -5 следует включить в область сходимости исследуемого степенного ряда.

Аналогичным образом исследуем сходимость степенного ряда в граничной точке х = 5, подставив в степенной ряд вместо х значение 5:

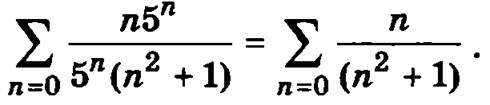
Применяя признак сравнения, рассмотрим поведение общего члена полученного числового ряда 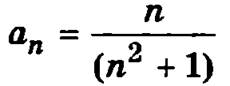для больших n. Пренебрегая в числителе единицей по сравнении с n2, получим 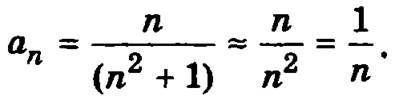Поэтому будем сравнивать данный числовой ряд с гармоническим рядом 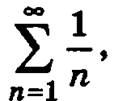который соответствует значению параметра s = 1, что означает его расходимость.

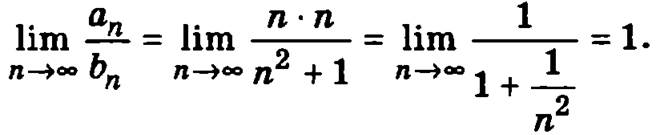
Рассмотренный предел конечен, и значит, что исследуемый числовой ряд будет расходиться вместе с рядом 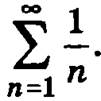Таким образом, точку х = 5 следует включить в область сходимости. Окончательно областью сходимости исходного степенного ряда будет множество [-5, 5).