Обыкновенные дифференциальные уравнения первого порядка - ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Обыкновенным дифференциальным уравнением называется соотношение, связывающее независимую переменную х, неизвестную функцию у(х) и ее производные F(x, y, у’, у’’,..., y(n)) = 0.

Порядком дифференциального уравнения называется наивысший порядок производной неизвестной функции, входящей в уравнение.

Например, уравнение у’’’ + ху’ = у3 третьего порядка, уравнение у(у’’)2 + у' cos х = 1 — дифференциальное уравнение второго порядка, уравнение 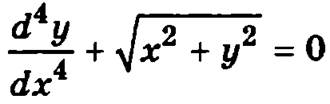— дифференциальное уравнение четвертого порядка.

Функция у(х), которая при подстановке в дифференциальное уравнение обращает его в тождество, называется решением дифференциального уравнения.

Решение дифференциального уравнения, заданное в неявном виде, называется интегралом дифференциального уравнения.

График функции, которая является решением дифференциального уравнения, называется интегральной кривой.

8.1. Обыкновенные дифференциальные уравнения первого порядка

Обыкновенным дифференциальным уравнением первого порядка называется соотношение, связывающее независимую переменную х, неизвестную функцию у(х) и ее первую производную F(x, у, у’) = 0.

Общим решением дифференциального уравнения первого порядка называется функция у = у(х, С), содержащая произвольную постоянную С и обращающая в тождество дифференциальное уравнение.

Частным решением дифференциального уравнения называется решение, которое получается из общего решения, если придать произвольной постоянной С некоторое числовое значение.

Геометрически общее решение дифференциального уравнения первого порядка можно представить, как семейство кривых в некоторой области D, каждая из которых соответствует определенному значению постоянной С, причем через каждую точку области D проходит только одна кривая семейства.

Иногда дифференциальное уравнение представляется в виде разрешенном относительно производной неизвестной функции у' = f(x, у).

Для того чтобы из семейства решений у = у(х, С) выделить единственное, к дифференциальному уравнению добавляют начальное условие — требование, чтобы интегральная кривая проходила через заданную точку (х0, у0) области D:

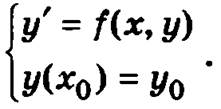
Задача определения решения дифференциального уравнения у' = f(x, у), удовлетворяющее условию y(x0) = y0, называется задачей Коши.

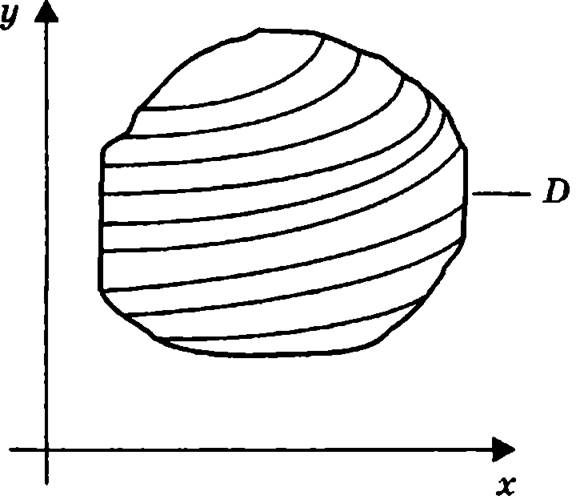
Рис. 13

Теорема существования и единственности решения дифференциального уравнения первого порядка

Если функция f(x, у) определена и непрерывна вместе с частной производной 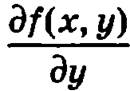во всех точках некоторой области D, то существует, и притом единственное, решение у = φ(х) дифференциального уравнения у' = f(х, у), проходящее через данную точку (x0, y0), принадлежащую области D, то есть удовлетворяющее условию у0 = φ(x0).