Математика 9 класс подготовка к ГИА
Вариант № 11 - Учебно-тренировочные тесты
Вариант № 11
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения ![]()
1) 1,.
2) 1.
3) 6,.
4) 66
2. На координатной прямой отмечены числа а и b (см. рис. 87).
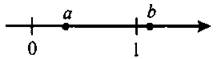
Рис. 87
Расположите в порядке возрастания числа 2a — b, a — b, b — а.

3. Сумма какого из указанных чисел с числом √5 является рациональным числом?
![]()
4. Решите уравнение 2х2 + 5х — 3 = 0.
Ответ: _________________.
5. Установите соответствие между графиками функций (см. рис. 88) и формулами, которые их задают.
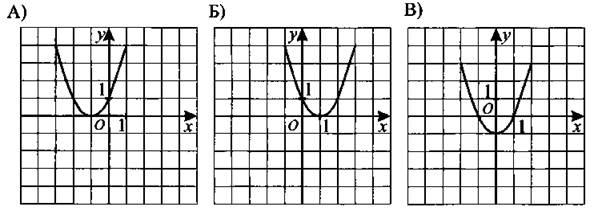
Рис. 88
1) у = (х — 1)2
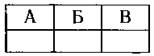
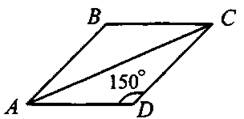
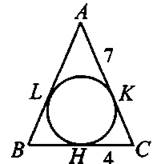
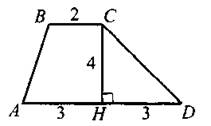
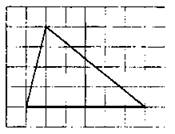
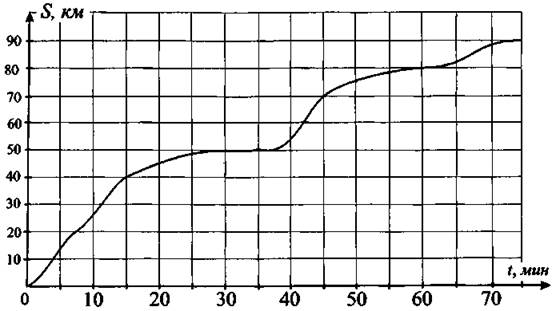
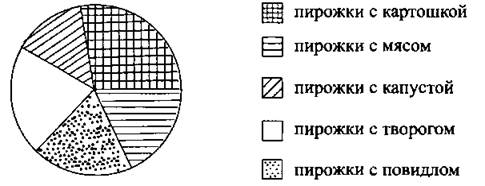
2) у = (х + 1)2 3) у = х2 — . 4) у = х2 + 1 Ответ: 6. Найдите разность арифметической прогрессии, если её второй и девятый члены равны 0,4 и 3,9 соответственно. Ответ: _________________. 7. Упростите выражение (а — 1)(а — 2) — а(а — 3), найдите его значение при a = 0,17. В ответе запишите полученное число. Ответ: _________________. 8. Решите систему неравенств На каком из рисунков изображено множество её решений? Модуль «Геометрия» 9. В ромбе ABCD угол ADC равен 150° (см. рис. 89). Найдите величину угла ВАС. Ответ дайте в градусах. Рис. 89 Ответ: _________________. 10. В равнобедренный треугольник с основанием ВС вписана окружность. Н, К, L — точки касания окружности со сторонами ВС, АС и АВ соответственно (см. рис. 90). Найдите периметр треугольника АВС, если НС = 4, АК = 7. Рис. 90 Ответ: _________________. 11. Найдите синус угла CDH (см. рис. 91). Рис. 91 Ответ: _________________. 12. Найдите площадь треугольника, изображённого на рисунке 92, если сторона квадратной клетки равна 1. Рис. 92 Ответ: _________________. 13. Укажите номера верных утверждений. 1) Если в равнобедренном треугольнике один из углов равен 60°, то такой треугольник — правильный. 2) В трапецию с основаниями 6 и 3 и боковыми сторонами 4 и 4 можно вписать окружность. 3) В любом треугольнике против большего угла лежит большая сторона. Ответ: _________________. Модуль «Реальная математика» 14. Рабочие пилили брёвна. Они сделали 8 распилов и получили 13 чурбачков. Сколько брёвен было изначально? Ответ: _________________. 15. На графике показана зависимость пройденного автомобилем расстояния от времени (см. рис. 93). На оси абсцисс откладывается время в минутах, на оси ординат — расстояние в километрах. Через сколько минут после начала движения автомобиль преодолеет расстояние, равное 70 км? Рис. 93 Ответ: _________________. 16. На субботнике сначала подмели 7 м2, потом ещё 3/4 оставшейся площади требуемого участка, после сделали перерыв. На перерыве ученики подсчитали, что им осталось подмести ещё 1/5 всего участка. Какова площадь участка, который необходимо подмести? Ответ дайте в м2. Ответ: _________________. 17. Робот сделал 60 шагов по прямой, затем повернулся на 90° против часовой стрелки и сделал ещё 25 шагов. На какое расстояние робот удалился от первоначального положения? Ответ дайте в шагах. Ответ: _________________. 18. В столовой подсчитали количество выпекаемых пирожков в неделю. Результаты представлены на круговой диаграмме (см. рис. 94). Рис. 94 Доля каких пирожков составляет более 25% от общего числа выпекаемых пирожков? 1) с творогом 2) с мясом 3) с картошкой 4) с повидлом 19. За сутки от остановки Васи до остановки его друга проходит 11 автобусов, 6 маршрутных такси и 3 троллейбуса (все они проходят через одинаковые промежутки времени). В произвольный момент суток Васе звонит друг и приглашает в гости, после чего Вася незамедлительно выходит на свою остановку и садится на первый подошедший транспорт. Какова вероятность того, что Вася поедет к другу на маршрутном такси? Ответ: _________________. 20. Высоту h, на которой окажется тело при свободном падении с высоты ho, можно приближённо вычислить по формуле h = h0 — v0t — 5t2, где v — начальная скорость (в м/с), t — время падения. С какой высоты нужно отпустить тело (v0 = 0), чтобы оно приземлилось через 3 с? Ответ дайте в метрах. Ответ: _________________. Часть 2 Задания этой части выполняйте с записью решения Модуль «Алгебра» 21. Решите неравенство 22. Мальчик поднялся по опускающемуся эскалатору и сразу же спустился по поднимающемуся эскалатору той же длины, затратив на эти действия 2,5 минуты. Длина эскалатора равна 150 ступенькам. Какова скорость мальчика (в ступеньках в секунду), если собственная скорость эскалатора равна 1 ступеньке в секунду? 23. Постройте график функции Модуль «Геометрия» 24. Биссектриса угла при вершине равнобедренного треугольника в 2 раза меньше основания этого треугольника. Найдите высоту, опущенную на боковую сторону, если длина боковой стороны равна 3. 25. Докажите, что диаметр вписанной в равнобедренный треугольник окружности не может быть равен основанию треугольника. 26. В прямоугольной трапеции ABCD с основаниями ВС = 1 и AD = 9 и боковой стороной АВ ⊥ ВС диагональ АС перпендикулярна боковой стороне CD. Найдите площадь трапеции.
![]()
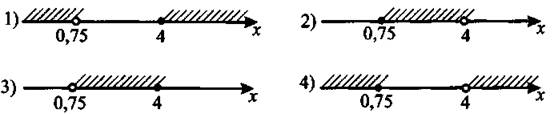
![]()
![]() Определите, при каких значениях параметра k прямая у = kх имеет с этим графиком ровно одну общую точку.
Определите, при каких значениях параметра k прямая у = kх имеет с этим графиком ровно одну общую точку.