Задания, содержащие параметр - Краткий теоретический справочник

Пусть дано уравнение вида f(a, x) = g(a, x), где а, х — переменные величины.

Переменная а, которая при решении этого уравнения считается постоянной, называется параметром, а само уравнение — уравнением, содержащим параметр.

Решить уравнение (с переменной х и параметром а) — значит на множестве действительных чисел решить семейство уравнений, получаемых из данного при всех допустимых значениях параметра а.

Многие уравнения с параметром могут быть решены с помощью следующего алгоритма.

1) Определить ограничения, налагаемые на значения неизвестного х и параметра а, исходя из того, что функции f(a, х) и g(а, х) имеют смысл.

2) Определить формальные решения уравнения, записываемые без учёта ограничений. Если при решении возникают контрольные значения параметра, то их наносят на числовую ось Оа. Эти значения разбивают область допустимых значений параметра на подмножества. На каждом из подмножеств решают заданное уравнение.

3) Исключить те значения параметра, при которых формальные решения не удовлетворяют полученным ограничениям.

4) На числовую ось Оа добавить значения параметра, найденные в п. 3. Для каждого из промежутков на оси Оа записать все полученные решения в зависимости от значений параметра а.

5) Записать ответ, то есть решения в зависимости от значений параметра а.

При решении заданий с параметрами часто встречаются задачи (или приводящие к ним) о расположении корней квадратного уравнения.

Пусть x₁ и x₂ — корни квадратного трёхчлена (x₁ < x₂) f(x) = ах² + bх + с, у которого D = b² — 4ас, а ≠ 0, x₀ = —b/2a и даны некоторые точки А и В оси Ох.

Утверждение 1. Оба корня меньше числа А, то есть х₁ < А и x₂ < А тогда и только тогда, когда

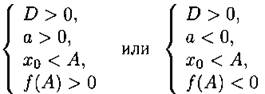(см. рис. 12).

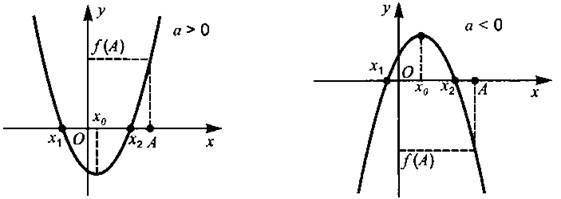
Рис. 12

Утверждение 2. Корни лежат по разные стороны от числа А, то есть х₁ < А < x₂, тогда и только тогда, когда

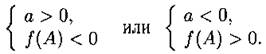
Утверждение 3. Оба корня больше числа А, то есть х₁ > А и x₂ > А, тогда и только тогда, когда

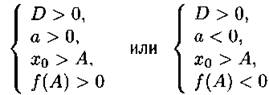(см. рис. 13).

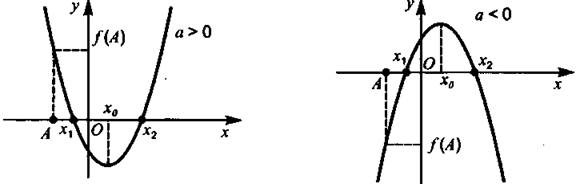
Рис. 13

Утверждение 4. Оба корня лежат между точками A и В, то есть А < x₁ < В и А < х₂ < В, тогда и только тогда, когда

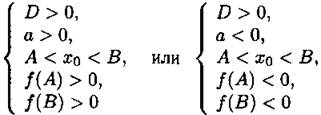(см. рис. 14).

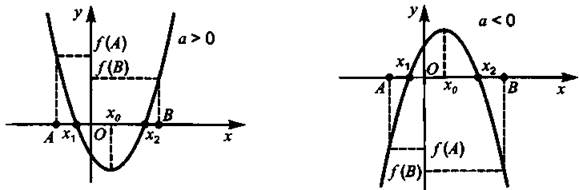
Рис. 14

Утверждение 5. Корни лежат по разные стороны от отрезка [A; В], то есть х₁ < А < В < х₂, тогда и только тогда, когда

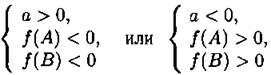(см. рис. 15).

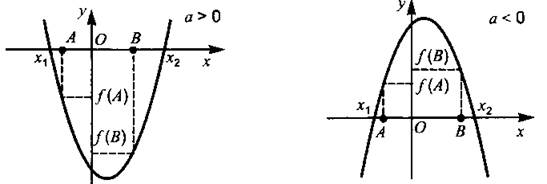
Рис. 15