Математика 9 класс подготовка к ГИА
Исследование функции и построение графика - Краткий теоретический справочник
Область определения функции.
Областью определения D(y) функции у = f(x) называется множество всех значений аргумента х, для которых выражение f(x) определено (имеет смысл).
Области определения основных элементарных функций. Область определения любого многочлена — R.
![]()
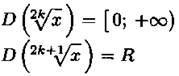
Множество значений функции.
Множеством (областью) значений Е(у) функции у = f(x) называется множество всех таких чисел уо, для каждого из которых найдется такое число хо, что f(x0) = у0.
Области значений основных элементарных функций.
Областью значений всякого многочлена чётной степени является промежуток [m; +∞), где m — наименьшее значение этого многочлена, либо промежуток [—∞; n], где n — наибольшее значение этого многочлена.
Областью значений всякого многочлена нечётной степени является R.
Чётность и нечётность функции.
Функция у = f(x) называется чётной, если для любого х ∈ D(f) верно равенство f(—x) = f(x). График чётной функции симметричен относительно оси Оу.
Функция у = f(x) называется нечётной, если для любого х ∈ D(f) верно равенство f(—x) = —f(x). График нечётной функции симметричен относительно начала координат.
Графики элементарных функций. На рисунке 1 изображены графики некоторых элементарных функций.
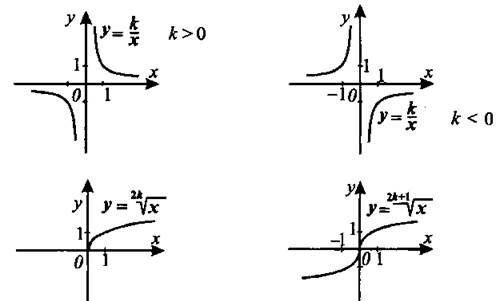
Рис. 1
Построение графиков функций «механическими» преобразованиями.
График функции у = -f(x) получен из графика функции у = f(x) отражением относительно оси Ох (см. рис. 2).
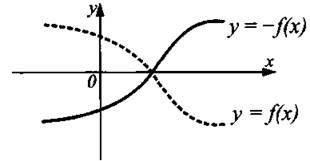
Рис. 2
График функции у = f(-x) получен из графика функции у = f(x) отражением относительно оси Оу (см. рис. 3).
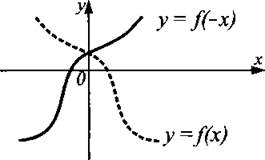
Рис. 3
График функции у = m ∙ f(x), m > 1, получен из графика функции у = f(x) растяжением в m раз вдоль оси Оу от оси Ох (см. рис. 4).
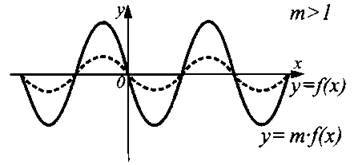
Рис. 4
График функции у = m ∙ f(x), 0 < m < 1, получен из графика функции у = f(x) сжатием в 1/m раз вдоль оси Оу к оси Ох (см. рис. 5).
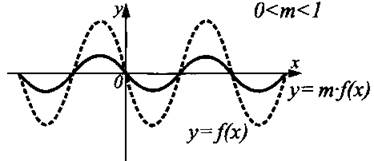
Рис. 5
График функции у = f(kx), k > 1, получен из графика функции у = f(x) сжатием в к раз к оси Оу вдоль оси Ох (см. рис. 6).
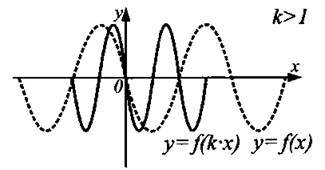
Рис. 6
График функции у = f(kx), 0 < k < 1, получен из графика функции у = f(x) растяжением в 1/k раз от оси Оу вдоль оси Ох (см. рис. 7).
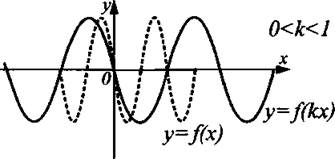
Рис. 7
График функции у = f(x) + b получен из графика функции у = f(x) сдвигом вверх на число b при b > 0 и сдвигом вниз на число (—b) при b < 0 (см. рис. 8).
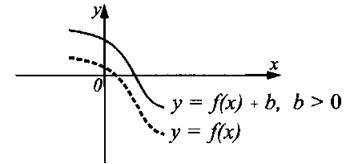
Рис. 8
График функции у = f(x + a) получен из графика функции у = f(x) сдвигом вправо на число —а при а < 0 и сдвигом влево на число а при а > 0 (см. рис. 9).
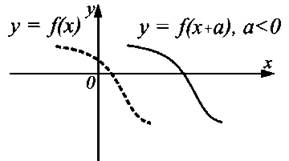
Рис. 9
График функции у = │f(x)│ (см. рис. 11, а) получен из графика функции у = f(x) (см. рис. 10) отражением относительно оси Ох части этого графика, лежащей ниже оси Ох.
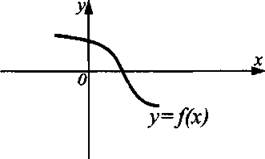
Рис. 10
График функции у = f(|x|) (см. рис. 11, б) получен из графика функции у = f(x) (см. рис. 10) объединением части этого графика, лежащей правее оси Оу, с её отражением относительно оси Оу и удалением части, лежащей левее оси Оу.
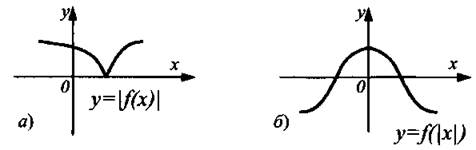
Рис. 11