Поурочные разработки по геометрии 9 класс
Произведение вектора на число - ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ
Цели: ввести понятие умножения вектора на число; рассмотреть основные свойства умножения вектора на число.
Ход урока
I. Изучение нового материала (лекция).
1. Целесообразно в начале лекции привести пример, подводящий к определению произведения вектора на число, в частности такой:
Автомобиль движется прямолинейно со скоростью ![]() . Его обгоняет второй автомобиль, двигающийся со скоростью, вдвое большей. Навстречу им движется третий автомобиль, у которого величина скорости такая же, как у второго автомобиля. Как выразить скорости второго и третьего автомобилей через скорость
. Его обгоняет второй автомобиль, двигающийся со скоростью, вдвое большей. Навстречу им движется третий автомобиль, у которого величина скорости такая же, как у второго автомобиля. Как выразить скорости второго и третьего автомобилей через скорость ![]() первого автомобиля и как изобразить с помощью векторов эти скорости?
первого автомобиля и как изобразить с помощью векторов эти скорости?
Ответ дает рисунок. Естественно считать, что скорость второго автомобиля равна 2![]() (произведению скорости
(произведению скорости ![]() первого автомобиля на число 2), а скорость третьего автомобиля равна –2
первого автомобиля на число 2), а скорость третьего автомобиля равна –2![]() (произведению скорости
(произведению скорости ![]() на число –2).
на число –2).
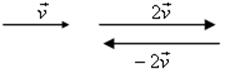
2. Определение произведения вектора на число, его обозначение: ![]() (рис. 260).
(рис. 260).
3. Записать в тетрадях:
1) произведение любого вектора на число нуль есть нулевой вектор;
2) для любого числа k и любого вектора ![]() векторы
векторы ![]() и
и ![]() коллинеарные.
коллинеарные.
4. Основные свойства умножения вектора на число:
Для любых чисел k, l и любых векторов ![]() справедливы равенства:
справедливы равенства:
1°. ![]() (сочетательный закон) (рис. 261);
(сочетательный закон) (рис. 261);
2°. ![]() (первый распределительный закон) (рис. 262);
(первый распределительный закон) (рис. 262);
3°. ![]() (второй распределительный закон) (рис. 263).
(второй распределительный закон) (рис. 263).
Примечание. Рассмотренные нами свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях.
Например.
![]()
![]()
II. Закрепление изученного материала.
1. Выполнить практические задания № 776 (б; г; д), 777.
2. Решить задачи № 779, 781 (а; в) на доске и в тетрадях.
Решение
Дано: ![]()
а) ![]()
в) 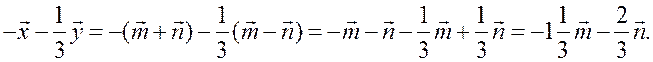
3. Решить задачу № 780 (б).
III. Итоги урока.
Домашнее задание: изучить материал пункта 83; ответить на вопросы 14–17, с. 214; решить задачи №№ 775, 776 (а, в, е), 781 (б), 780 (а).