Площадь кругового сектора - ДЛИНА ОКРУЖНОСТИ. ПЛОЩАДЬ КРУГА

Цели: ввести понятие кругового сектора, вывести формулу для вычисления площади кругового сектора; научить применять знания при решении задач.

Ход урока

I. Проверка изученного материала.

1. Формула длины окружности. Выражение радиуса окружности через длину окружности.

2. Формулы площади круга, радиуса круга через площадь круга, формула площади круга, выраженная через диаметр круга.

3. Формула длины дуги окружности.

4. Устно решить задачу № 1115.

 

II. Объяснение нового материала.

1. Ввести понятие кругового сектора и понятие дуги сектора (рис. 315).

2. Вывести формулу для вычисления площади S кругового сектора радиуса R, ограниченного дугой с градусной мерой .

Так как площадь всего круга равна πR2, то площадь кругового сектора, ограниченного дугой в 1°, равна .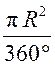

Поэтому площадь S выражается формулой S =∙ 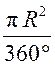

3. Ввести понятие кругового сегмента и познакомить учащихся с нахождением площади кругового сегмента, используя таблицу «Круговой сегмент».

 

III. закрепление изученного материала (решение задач).

1. Решить задачу.

АВСD – квадрат со стороной 1 дм. Найдите площадь «чечевицы», заштрихованной на рисунке.

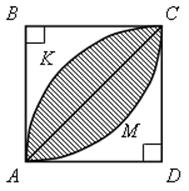
Решение

Так как сторона квадрата равна 1 дм, то площадь квадрата АВСD равна 1 дм2.

Площадь сектора DАKС равна 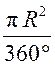∙ 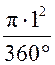 = ∙ 90° = (дм2).

Площадь треугольника АСD равна дм2.

Площадь сегмента АKС равна 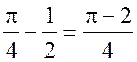(дм2).

Площадь «чечевицы»: 2 ∙ 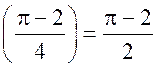≈ 0,7 (дм2).

Ответ: 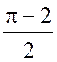≈ 0,7 дм2.

2. Решить задачу № 1126 (самостоятельно).

Решение

R = 10 см; Sкруга = πR2 = 100π (см2).

l =  = 60°; Sсектора =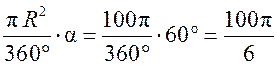 (см2).

S = Sкруга – Sсектора = 100π –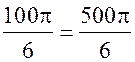≈ 262 (cм2).

Ответ: ≈ 262 см2.

3. Решить задачу № 1127.

Решение

 = 72°, Sсектора = S. Найти: R.

S =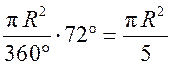; 5S = πR2; R2 =; R =.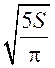

Ответ: .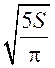

4. Вывести формулу площади кольца, ограниченного двумя окружностями с общим центром и радиусами R1 и R2, где R1 < R2.

Решени.

; Sкольца = S2 – S1 = .

5. Решить задачу № 1120.

Решение

R1 = 1,5 cм, R2 = 2,5 см.

Sкольца = π (2,52 – 1,52) = π (2,5 – 1,5) (2,5 + 1,5) = π ∙ 1 ∙ 4 = 4π (см2).

Ответ: 4π см2.

6. Решить задачу № 1122 на доске и в тетрадях.

Решение

R1 = 3 м, R2 = 3 + 1 = 4 (м).

Sдорожки = π = π (42 – 32) = π (4 – 3) (4 + 3) = 7π (м2).

На 1 м2 дорожки требуется 0,8 дм3 песка; тогда 0,8 ∙ 7π = 5,6π (дм3) ≈ 17,6 дм3.

Ответ: ≈ 17,6 дм3.

 

IV. Итоги урока.

Домашнее задание: выучить материал пунктов 110–112; повторить материал пунктов 105–109; ответить на вопросы 1–12 на с. 290; решить задачи № 1121, 1128, 1124.