Связь между координатами вектора и координатами его начала и конца. Простейшие задачи в координатах - МЕТОД КООРДИНАТ

Цели: рассмотреть связь между координатами вектора и координатами его начала и конца; разобрать задачи о нахождении координат середины отрезка, о вычислении длины вектора по его координатам и нахождении расстояния между двумя точками.

Ход урока

I. Анализ результатов контрольной работы.

1. Указать ошибки, сделанные учащимися при выполнении работы.

2. Решить на доске задачи, вызвавшие затруднения у учащихся.

II. Изучение нового материала (лекция).

1. Рассмотреть по учебнику рис. 277 и рис. 278 и ввести понятие радиус-вектора .

Без доказательства записать в тетрадях утверждения:

а) координаты точки М равны соответствующим координатам ее радиус-вектора;

б) каждая координата вектора равна разности соответствующих координат его конца и начала:

џ Устно решить задачу № 934.

2. Введение системы координат дает возможность изучать геометрические фигуры и их свойства с помощью уравнений и неравенств и, таким образом, использовать в геометрии методы алгебры. Такой подход к изучению свойств геометрических фигур называется методом координат.

3. Рассмотрим три вспомогательные задачи.

1) Координаты середины отрезка.

Используя формулу из п. 84 (1) 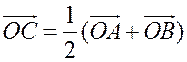и координаты векторов записать равенство в координатах: 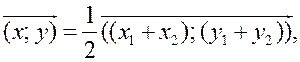отсюда x = 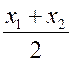; y = .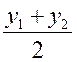

Вывод: каждая координата середины отрезка равна полусумме соответствующих координат его концов.

џ Устно решить задачу № 936.

2) Вычисление длины вектора по его координатам.

Используя рис. 280 учебника, вывести формулу , если

џ Устно решить задачу № 938.

3) Расстояние между двумя точками.

Пусть точка M1 (x1; y1) и точка M2 (x2; y2); тогда вектор (x2 – x1; y2 – y1); следовательно, длина этого вектора может быть найдена по формуле 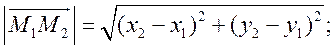но = d, таким образом, расстояние d между точками M1 (x1; y1) и M2 (x2; y2) выражается формулой d =

џ Решить задачу № 940 (а, б) на доске и в тетрадях.

III. Закрепление изученного материала (решение задач).

1. Решить задачу № 939.

Решение

Найти расстояние от точки М (3; –2): а) до оси абсцисс; точка В (x; y) лежит на оси абсцисс; тогда расстояние равно 2; б) расстояние до оси ординат равно 3; в) до начала координат равно d =

2. Решить задачу № 941 на доске и в тетрадях.

Решение

PΔ = MN + NP + MP;

MN =

NP =

MP =

PΔMNP = .

IV. Итоги урока.

Задание на дом: изучить материал пунктов 88, 89; решить задачи №№ 935, 952.