Поурочные разработки по геометрии 9 класс
Координаты вектора - МЕТОД КООРДИНАТ
Цели: ввести понятие координат вектора и рассмотреть правила действий над векторами с заданными координатами.
Ход урока
I. Проверка домашнего задания.
1. Устно решить задачи:
1) назвать числа х и у, удовлетворяющие равенству: ![]() ;
; ![]() ;
;
2) задача № 913.
2. На доске двое учащихся решают задачи №№ 911 (в) и 912 (и, к).
II. Изучение нового материала.
1. Напомнить задание прямоугольной системы координат и начертить ее.
2. Ввести координатные векторы ![]() и
и ![]() (рис. 275).
(рис. 275).
3. Нулевой вектор можно представить в виде ![]() ; его координаты равны нулю:
; его координаты равны нулю: ![]() (0; 0).
(0; 0).
4. Координаты равных векторов соответственно равны.
5. Рассмотреть правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число (доказательства указанных правил учащиеся могут рассмотреть самостоятельно).
6. Записать в тетрадях правила:
![]() и
и ![]() – данные векторы
– данные векторы
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
III. Закрепление изученного материала (решение задач).
1. Решить задачу № 917 на доске и в тетрадях.
2. Устно по рисунку 276 решить задачу № 918.
3. Решить задачу № 919 (самостоятельно).
4. Решить задачу № 920 (а, в) на доске и в тетрадях.
5. Устно решить задачи № 922–925, используя правила, записанные в тетрадях.
6. Записать утверждение задачи № 927 без доказательства:
1) Если два вектора коллинеарные, то координаты одного вектора пропорциональны координатам другого: если ![]() коллинеарен вектору
коллинеарен вектору ![]() , то x1 : x2 = y1 : y2.
, то x1 : x2 = y1 : y2.
2) Если координаты одного вектора пропорциональны координатам другого вектора, то эти векторы коллинеарные.
7. Решить задачу № 928.
Решение
Используем условие коллинеарности векторов: 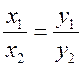 .
.
1) ![]() (3; 7) и
(3; 7) и ![]() (6; 14), так как
(6; 14), так как 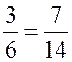 ;
;
2) ![]() (–2; 1) и
(–2; 1) и ![]() (2; –1), так как
(2; –1), так как 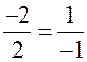 .
.
IV. Самостоятельная работа контролирующего характера.
Вариант I
Решить задачи № 912 (а, г); № 920 (г); № 988 (а, б); № 921 (а, в); № 914 (а).
Вариант II
Решить задачи №№ 912 (в, д); 920 (д); 988 (в, г); 921 (б, г); 914 (б).
V. Итоги урока.
Домашнее здание: подготовиться к устному опросу по карточкам, повторить материал пунктов 76–87; ответить на вопросы 1–20, с. 213–214 и на вопросы 1–8, с. 249 учебника; решить задачи №№ 798, 795; 990 (а) (для векторов ![]() и
и ![]() ).
).