Уроки-конспекты по Геометрии 8 класс
ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА - урок 3
Цели: рассмотреть теорему о точке пересечения высот треугольника.
Ход урока
I. Проверка домашнего задания.
Решить устно:
1. Найти: РВKС, РАВС.
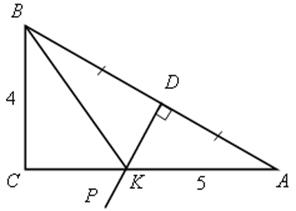
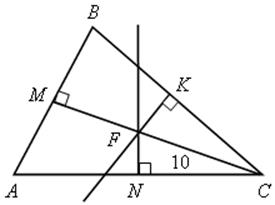
2. FK, FN серединные перпендикуляры.
АВ = 16
СF = 10
Найти расстояние от точки F до стороны АВ.
II. Изучение нового материала.
Теорему о точке пересечения высот треугольника учителю желательно прокомментировать по заранее заготовленному чертежу, а детальное доказательство предложить учащимся провести дома самостоятельно или с помощью учебника.
III. Закрепление изученного материала.
1. Решить устно:
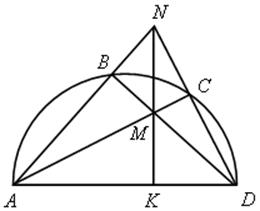
Дуга АD – полуокружность.
Доказать MN ![]() АD.
АD.
2. Решить №№ 677, 684, 687.
№ 677.
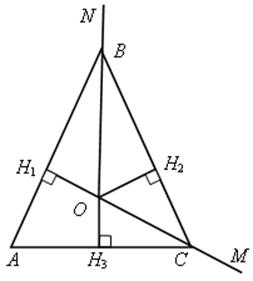
Решение
1) ![]() АВО = 180° –
АВО = 180° – ![]() АВN = 180° –
АВN = 180° – ![]() СВN =
СВN = ![]() CВО, то есть ВО – биссектриса
CВО, то есть ВО – биссектриса ![]() АВС, аналогично СО – биссектриса
АВС, аналогично СО – биссектриса ![]() АСВ.
АСВ.
2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 ![]() АВ, ОН2
АВ, ОН2 ![]() ВС, ОН3
ВС, ОН3 ![]() АС.
АС.
2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН1.
№ 684.
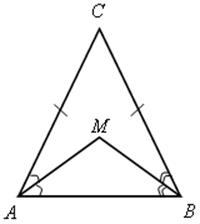
Решение
1) По свойству углов при основании равнобедренного треугольника ![]() САВ =
САВ = ![]() СВА.
СВА.
Тогда ![]() МАС =
МАС = ![]() МАВ =
МАВ = ![]()
![]() САВ =
САВ = ![]()
![]() СВА =
СВА =![]() МВС =
МВС = ![]() МВА.
МВА.
2) ![]() МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.
МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.
3) Так как АС = СВ, то точка С также лежит на серединном перпендикуляре к АВ. Таким образом, СМ ![]() АВ.
АВ.
№ 687.
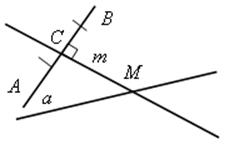
Решение
1) Построим серединный перпендикуляр m к отрезку АВ.
2) Точка М – точка пересечения m c а.
3) М – искомая.
Задача имеет решение в случае, если прямая АВ не перпендикулярна к данной прямой а.
IV. Итоги урока.
Четыре замечательные точки треугольника.
1) О – точка пересечения медиан треугольника АВС.
АМ : МА1 = ВМ = МВ1 = СМ = МС1 = 2 : 1.
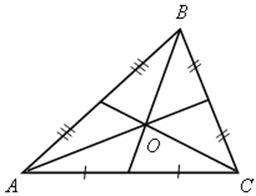
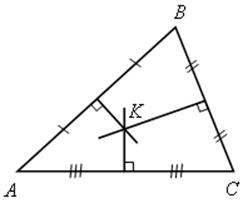
2) K – точка пересечения серединных перпендикуляров к сторонам треугольника АВС.
АK = KС = KВ.
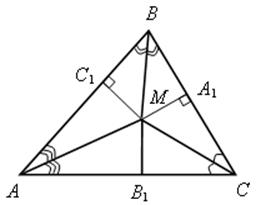
3) М – точка пересечения биссектрис углов треугольника АВС.
МС1 = МА1 = МВ1.
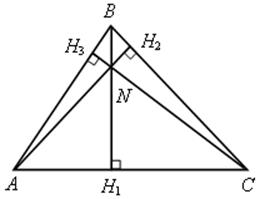
4) N – точка пересечения высот треугольника (или их продолжений).
Домашнее задание: вопросы 1– 20, с. 187–188; №№ 688, 720.
Рекомендовать решать № 720 методом от противного.
Для желающих.
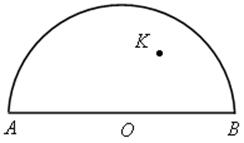
Полуокружность с концами АВ и отмечена точка K. С помощью одной линейки постройте прямую, проходящую через точку K и перпендикулярную к прямой АВ.
Использовать решение и чертеж устной задачи урока.