Уроки-конспекты по Геометрии 8 класс
ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ - урок 3
Цели: рассмотреть теорему об отрезках пересекающихся хорд и применение изученного материала при решении задач.
Ход урока
I. Проверка домашнего задания.
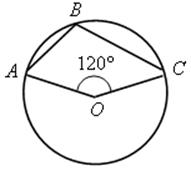
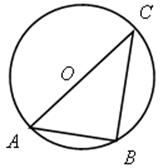
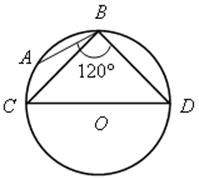
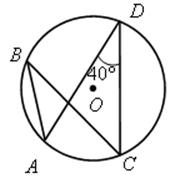
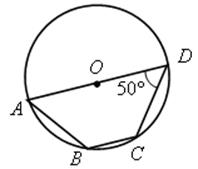
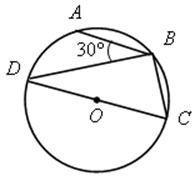
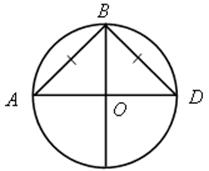
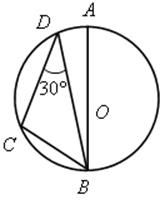
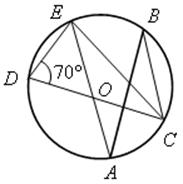
1. Найти градусную меру угла АВС (устно):
|
|
|
|
|
|
|
|
|
2. Рассмотреть решение задачи № 664.
II. Изучение нового материала.
1. Докажите, что ![]() АМС
АМС ![]()
![]() DМВ.
DМВ.
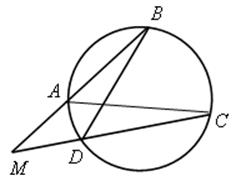
2. Доказать теорему о произведении отрезков пересекающихся хорд.
III. Закрепление изученного материала.
Решить №№ 666 (а; б), 668, 670, 671 (а), 673.
№ 668.
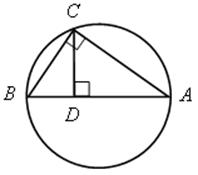
Решение
1) ![]() АСВ – вписанный и опирается на полуокружность, следовательно,
АСВ – вписанный и опирается на полуокружность, следовательно, ![]() АСВ = 90°.
АСВ = 90°.
2) СD = ![]() .
.
№ 670.
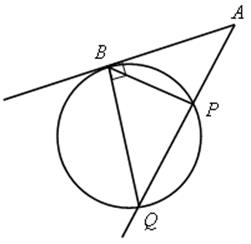
Решение
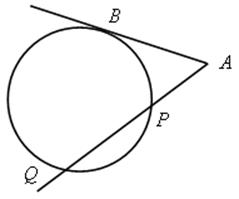
1) ![]() АВР =
АВР = ![]() АQВ, так как
АQВ, так как ![]() АВР =
АВР = ![]()
![]() ВР (задача № 664) и
ВР (задача № 664) и ![]() АQВ =
АQВ = ![]()
![]() BP.
BP.
2) ![]() АВР
АВР ![]()
![]() АQB по двум углам (угол А – общий и
АQB по двум углам (угол А – общий и ![]() АВР =
АВР = ![]() АQB).
АQB).
3) 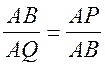 , AB2 = AP · AQ.
, AB2 = AP · AQ.
№ 671 (а). Для решения использовать задачу № 670.
№ 672.
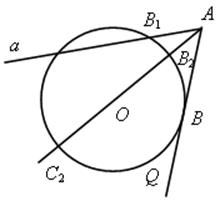
Решение
1. Проведем касательную к окружности через точку А. Имеем АВ – касательная к окружности.
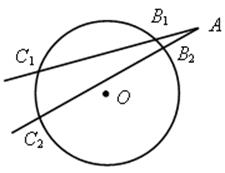
2. АС1 и АВ – секущая и касательная, значит, АВ2 = АВ1 · АС1
3. АС2 и АВ – секущая и касательная, поэтому АВ2 = АВ2 · АС2.
4. АВ1 · АС1 = АВ2 · АС2.
IV. Итоги урока.
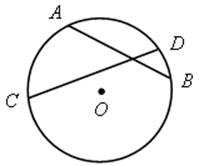
1) АD и СВ – хорды; АЕ · ЕD = СЕ · ЕD.
2) АС – касательная; АВ – хорда; ![]() САВ =
САВ = ![]()
![]() АВ.
АВ.
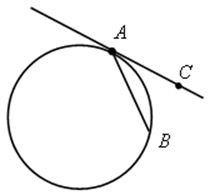
3) АВ – касательная; AQ – секущая; АВ2 = АР · AQ.
4) АС1 и АС2 – секущие; АВ1 · AС1 = АВ2 · АС2.
Домашнее задание: вопросы 1–14, с. 187; №№ 666 (б), 667, 671; подготовиться к самостоятельной работе.
Для желающих: № 718 (решение в учебном пособии, с. 188–189) и задача.
Задача.
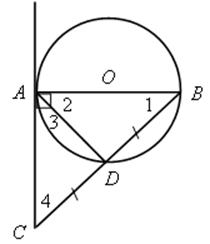
Через конец В диаметра АВ проведена секущая, которая пересекается в точке D с касательной, проведенной через другой конец диаметра А; радиус окружности равен 3 см. Найти длину отрезка касательной АD, если известно, что секущая ВD в точке пересечения с окружностью делится пополам.
Решение
1. ![]() 3 =
3 = ![]()
![]() AD,
AD, ![]() 1 =
1 = ![]()
![]() AD,
AD, ![]() 1 =
1 = ![]() 3.
3.
2. ![]() АDС:
АDС: ![]() 3 +
3 + ![]() 4 +
4 + ![]() АDС = 180°;
АDС = 180°;
Из ![]() АВС:
АВС: ![]() 4 = 90° – 1; но
4 = 90° – 1; но ![]() 1 =
1 = ![]() 3, поэтому
3, поэтому ![]() 4 = 90° –
4 = 90° – ![]() 3.
3.
Имеем ![]() 3 + 90° –
3 + 90° – ![]() 3 +
3 + ![]() АDС = 180°
АDС = 180°
![]() АDС = 90°.
АDС = 90°.
3. Получили ![]() АВС равнобедренный, так как АD – медиана и высота.
АВС равнобедренный, так как АD – медиана и высота.
4. АВ = АС = 6 см.
№ 667.
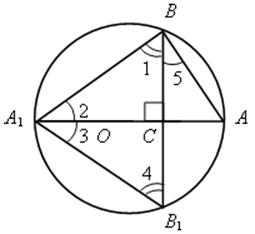
Решение
1) ![]() АВА1 – прямоугольный, так как вписанный угол А1ВА опирается на полуокружность.
АВА1 – прямоугольный, так как вписанный угол А1ВА опирается на полуокружность.
2) ![]() 5 =
5 = ![]() 3 как вписанные и опирающиеся на одну дугу АВ1.
3 как вписанные и опирающиеся на одну дугу АВ1.
3) ![]() 1 = 90° –
1 = 90° – ![]() 5,
5, ![]() 4 = 90° –
4 = 90° – ![]() 3, но
3, но ![]() 3 =
3 = ![]() 5, поэтому
5, поэтому ![]() 1 =
1 = ![]() 4.
4.
4) ![]() А1ВВ1 – равнобедренный, тогда ВС = В1С.
А1ВВ1 – равнобедренный, тогда ВС = В1С.
5) По теореме о произведении отрезков пересекающихся хорд АС · А1С = ВС · В1С.
ВС2 = АС · А1С, ВС = ![]() .
.
6) ВС = ![]() (см); BB1 = 8
(см); BB1 = 8![]() (см).
(см).