Уроки-конспекты по Геометрии 8 класс
ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ
Цель: рассмотреть градусную меру дуги окружности.
Ход урока
I. Анализ самостоятельной работы.
II. Объяснение нового материала.
Материал лучше дать в виде короткой лекции. Желательно, чтобы в тетрадях учащихся остался конспект этой лекции.
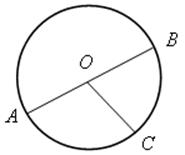
![]() АОС,
АОС, ![]() ВОС,
ВОС, ![]() АОВ – центральные углы;
АОВ – центральные углы;
![]() АВ и
АВ и ![]() АСВ – полуокружности;
АСВ – полуокружности;
![]() АС и
АС и ![]() ВС меньше полуокружности;
ВС меньше полуокружности;
![]() ВАС и
ВАС и ![]() АВС больше полуокружности;
АВС больше полуокружности;
![]() АС =
АС = ![]() АОС;
АОС; ![]() ВС=
ВС= ![]() ВОС;
ВОС; ![]() АВ =
АВ = ![]() АСВ =
АСВ = ![]() АОВ.
АОВ.
![]() ВАС = 360° –
ВАС = 360° – ![]() ВОС;
ВОС; ![]() АВС = 360° –
АВС = 360° – ![]() АОС;
АОС;
![]() АС +
АС + ![]() АВС =
АВС = ![]() АОС + (360° –
АОС + (360° – ![]() АОС) = 360°.
АОС) = 360°.
III. Закрепление изученного материала.
Решить № 650 (а, в) – устно, № 651 (а), № 716.
№ 716.
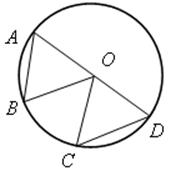
Решение
![]() АВ =
АВ = ![]() АОВ,
АОВ, ![]() СD =
СD = ![]() СОD, по условию
СОD, по условию ![]() АВ =
АВ = ![]() СD, следовательно,
СD, следовательно, ![]() АОВ =
АОВ = ![]() СОD.
СОD.
Поэтому ![]() АОВ =
АОВ = ![]() СОD по двум сторонам и углу между ними.
СОD по двум сторонам и углу между ними.
(АО = ВО = СО = DО и ![]() АОВ = ОD.) Тогда АВ = СD.
АОВ = ОD.) Тогда АВ = СD.
IV. Итоги урока.
Домашнее задание: вопросы 8, 9, 10, с. 187; №№ 650 (б), 651 (б), 652.
Для желающих.
1. Из точки, кратчайшее расстояние которой до окружности равно 25 мм, проведена к окружности касательная. Отрезок этой касательной между данной точкой и точкой касания равен 35 мм. Найти длину диаметра окружности.
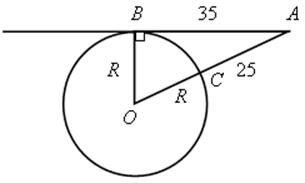
Решение
![]() АОВ,
АОВ, ![]() В = 90°.
В = 90°.
По теореме Пифагора
ОА2 = ОВ2 + АВ2
(R + АC)2 = R2 + АВ2
(R + 25)2 = R2 + 352
R2 + 50R + 625 = R2 + 1225
R = 12.
Длина диаметра равна 24 мм.
2. Из точки, наибольшее расстояние которой до окружности 50 мм, проведена к окружности касательная. Отрезок этой касательной между точкой касания и данной точкой равен 40 мм. Найти длину диаметра окружности.
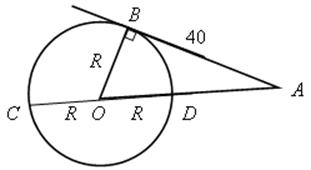
Решение
![]() АВО,
АВО, ![]() В = 90°.
В = 90°.
По теореме Пифагора
ОА2 = АВ2 + ОВ2
(50 – R)2 = 402 + R2
2500 – 100R + R2 = 1600 + R2
R = 9
Длина диаметра окружности 18 мм.