ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ - урок 3

Цели: закрепить навыки в решении задач на применение признаков и свойств параллелограмма; проверить знания учащихся по этой теме.

Ход урока

I. Проверка домашнего задания.

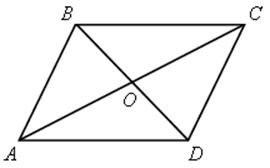
АВСD – параллелограмм:

а) Найти все углы АВD, если А = 42°.

б) Сумма двух из них равна 112°.

в) Найти периметр треугольника ВОА, если DС = 10 см, ВD = 18 см, АС = 20 см.

г) В окружности проведены диаметры АВ и СD. Докажите, что АВСD – параллелограмм.

II. Решение задач.

№ 372 (б).

Решение

Пусть АВ = х см, а ВС = (х + 7) см.

Так как периметр параллелограмма 48 см, имеем уравнение:

х + х + 7 = ,

2х + 7 = 24,

2х = 14,

х = 7.

Ответ: АВ = 7 см, ВС = 14 см.

№ 373.

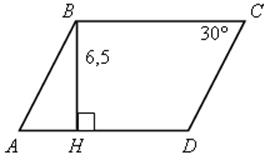
Решение

1) А = С по свойству параллелограмма.

2) АВН – прямоугольный; катет ВН лежит против угла в 30°, поэтому гипотенуза АВ в два раза больше него. Итак, АВ = 13 см. ВС = (50 – 13 · 2) : 2 = 12 см.

Ответ: 12, 13 см.

№ 374.

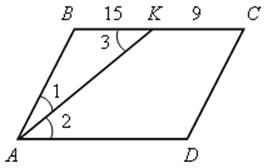
Решение

1) 1 = 2, так как АК – биссектриса, 2 = 3 как внутренние накрест лежащие углы при ВС || АD и секущей АK. Имеем 1 = 2 = 3.

2) АВK – равнобедренный, так как 1 = 3. Получили АВ = ВK = 15 см.

3) ВС = ВK + KС = 15 + 9 = 24 (см).

4) РАВСD = (15 + 24) · 2 = 78 (см).

Ответ: 78 см.

III. Самостоятельная работа.

Вариант I

1. В параллелограмме АВСD диагонали равны 8 см и 5 см, сторона ВС равна 3 см, О – точка пересечения диагоналей. Чему равен периметр треугольника АОD?

2. В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Докажите, что DЕС равнобедренный.

3. АС и ВD – диаметры окружности с центром О. Докажите, что А, В, С и D – вершины параллелограмма.

Вариант II

1. Определите стороны параллелограмма, если его периметр равен 38 дм, а одна из сторон на 11 дм больше другой.

2. В параллелограмме ВСDЕ диагонали пересекаются в точке М. Найдите периметр ВМС, если DЕ = 7 см, ВD = 12 см, СЕ = 16 см.

3. В параллелограмме ВDЕF на сторонах ВF и DЕ отложены равные отрезки ВО и DN. Докажите, что четырехугольник ONEF также является параллелограммом.

Домашнее задание: вопросы 6–9, с. 114; №№ 420, 425; повторить п. 25, 29.