Уроки-конспекты по Геометрии 8 класс
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА - урок 3
Цели: повторить и обобщить изученный материал, выработать умение учащихся применять изученный материал при решении задач; подготовить учащихся к контрольной работе.
Ход урока
I. Проверка домашнего задания.
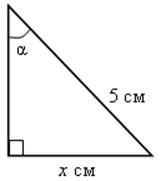
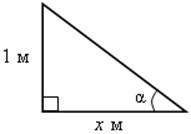
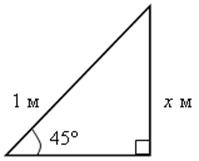
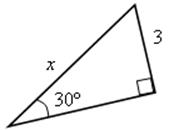
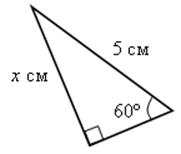
Выполнить задания устно: найти х.
1) |
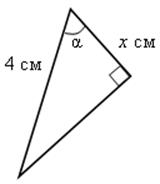
2) |
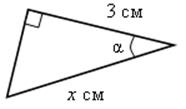
3) |
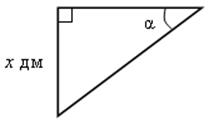
4) |
5) |
6) |
7) |
8) |
9) |
II. Решение задач.
№ 601.
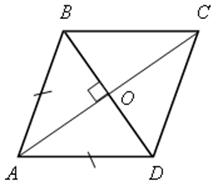
Решение
1) ![]() АОВ =
АОВ = ![]() СОВ =
СОВ = ![]() СОD =
СОD = ![]() АОD (по двум катетам).
АОD (по двум катетам).
2) tg![]() BCO =
BCO = 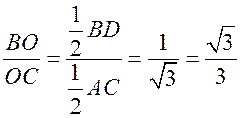 .
. ![]() BCO = 30°.
BCO = 30°.
3) ![]() ОBC = 90° –
ОBC = 90° – ![]() BCO = 90° – 30° = 60°.
BCO = 90° – 30° = 60°.
4) ![]() BCD = 2
BCD = 2![]() BCО = 30 · 2 = 60° =
BCО = 30 · 2 = 60° = ![]() BАD.
BАD.
5) ![]() АBC = 2
АBC = 2![]() ОBC = 60 · 2 = 120° =
ОBC = 60 · 2 = 120° = ![]() АDС.
АDС.
№ 602.
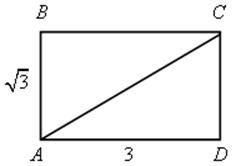
Решение
1) tg![]() BCА =
BCА = 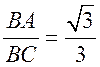 ;
; ![]() BCА = 30°.
BCА = 30°.
2) ![]() BАС = 90° – 30° = 60°.
BАС = 90° – 30° = 60°.
3) ![]() САD =
САD = ![]() BСА = 30°.
BСА = 30°.
4) ![]() DСА =
DСА = ![]() BАС = 60°.
BАС = 60°.
III. Самостоятельная работа.
Вариант I
В равнобедренной трапеции меньшее основание равно 4 см, боковая сторона равна 6 см, а один из углов трапеции равен 150°. Найдите площадь трапеции.
Вариант II
В прямоугольной трапеции меньшее основание равно 3 см, большая боковая сторона 4 см, а один из углов трапеции равен 150°. Найдите площадь трапеции.
Вариант III
(для более подготовленных учащихся)
В треугольнике АВС АС = ВС, cos β = ![]() . Найдите отношение высот АМ и CN треугольника АВС.
. Найдите отношение высот АМ и CN треугольника АВС.
Можно проверить решение на этом же уроке с помощью закрытой доски.
Вариант I
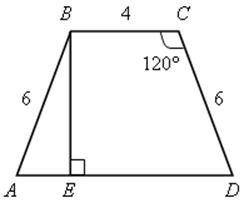
Решение
1) ![]() B =
B = ![]() С = 120°.
С = 120°.
![]() АBЕ = 120° – 90° = 30°.
АBЕ = 120° – 90° = 30°.
соs![]() АBЕ =
АBЕ = ![]() .
.
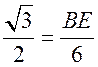 ; BE = 3
; BE = 3![]() (см).
(см).
2) sin![]() АBЕ =
АBЕ = 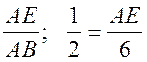 ; AE = 3 (см).
; AE = 3 (см).
3) АD = ВС + 2АЕ = 4 + 2 · 3 = 10 (cм).
4) SАВСD = 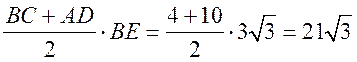 (см2).
(см2).
Вариант II
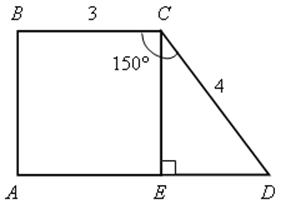
Решение
1) ![]() ЕCD =
ЕCD = ![]() BCD –
BCD – ![]() BCЕ = 150° – 90° = 60°.
BCЕ = 150° – 90° = 60°.
sin![]() ЕСD =
ЕСD = 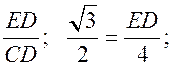 ED = 2
ED = 2![]() (см).
(см).
2) сos![]() ЕCD =
ЕCD = ![]() ;
; 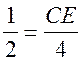 ; CE = 2 (см).
; CE = 2 (см).
3) АD = ВС + ЕD = 3 + 2![]() .
.
4) SАВСD = 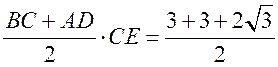 ∙ 2 = 6 + 2
∙ 2 = 6 + 2![]() (см2).
(см2).
Вариант III
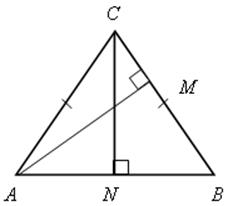
Решение
1) ![]() АМВ,
АМВ, ![]() М = 90°, сos
М = 90°, сos![]() В =
В = 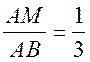 ; AM =
; AM = ![]() ;
;
2) ![]() СNВ,
СNВ, ![]() N = 90°, сos
N = 90°, сos![]() В =
В = 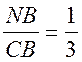 ;
; 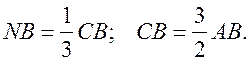
3) sin![]() В =
В = ![]() ;
; 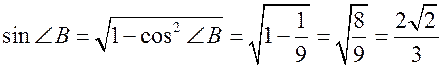 ;
; 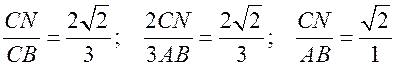 ;
; ![]() .
.
4) 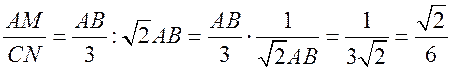 .
.
IV. Итоги урока.
Домашнее задание: вопросы 8–18, с. 160–161; №№ 603, 621, 626; подготовиться к контрольной работе.
Для желающих.
Радиомачта укреплена стальными канатами, наклоненными к земле под углом в 64°. Основание каждого каната удалено от мачты на 350 м. На какой высоте укреплены на мачте верхние концы канатов?
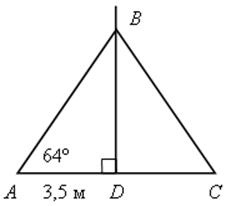
Решение
![]() АВD,
АВD, ![]() D = 90°, tg
D = 90°, tg![]() А =
А = ![]() ; BD = AD tg
; BD = AD tg![]() А,
А,
ВD = 3,5 · 2,05 ≈ 7,2 (м).