Уроки-конспекты по Геометрии 8 класс
ОПРЕДЕЛЕНИЕ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ - урок 2
Цели: ввести определение подобных треугольников; доказать теорему об отношении площадей подобных треугольников и рассмотреть применение их при решении задач.
Ход урока
I. Проверка домашнего задания.
1. Устно:
SBMN = 7 см2.
SАBС – ?
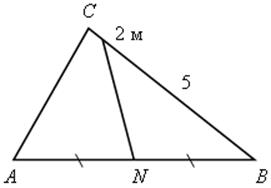
Ответ: 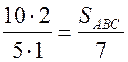 .
.
SАBС = 28 см2.
2. 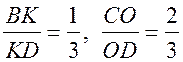 .
.
SАОС = 4 см2.
SBОK – ?
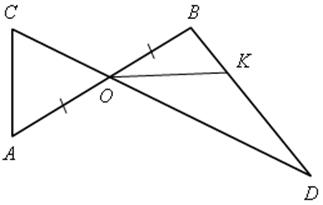
1) 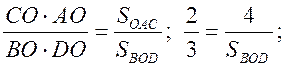 SBОD = 6 см2;
SBОD = 6 см2;
2) 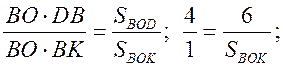 SBОK = 1,5 см2.
SBОK = 1,5 см2.
II. Изучение нового материала.
1. Ввести определение подобных треугольников.
2. Решить задачи устно:
а) ![]() АВС
АВС ![]()
![]() А1В1С1,
А1В1С1, ![]() А = 30°,
А = 30°, ![]() В = 85°,
В = 85°, ![]() С = 65°.
С = 65°.
Чему равны ![]() А1,
А1, ![]() В1,
В1, ![]() С1?
С1?
б) ![]() АВС
АВС ![]()
![]() С1А1В1, АВ = 3 см, ВС = 4 см, АС = 6 см, А1В1 = 12 см.
С1А1В1, АВ = 3 см, ВС = 4 см, АС = 6 см, А1В1 = 12 см.
Вычислите В1С1 и А1С1.
Ответ: В1С1 = 18 см, А1С1 = 9 см.
3. Доказательство теоремы об отношении площадей подобных треугольников.
III. Закрепление изученного материала.
№№ 544, 545, 548.
№ 545.
Решение
![]() АВС
АВС ![]()
![]() А1В1С1
А1В1С1
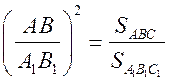 ;
;
Пусть ![]() = x, тогда SАВС = х + 77.
= x, тогда SАВС = х + 77.
Имеем 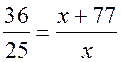 ;
;
36х = 25х + 77 · 25
11х = 77 · 25
х = 7 · 25
х = 175.
Ответ: ![]() = 175 см2, SАВС = 252 см2.
= 175 см2, SАВС = 252 см2.
№ 548.
Решение
![]() АВС
АВС ![]()
![]() А1В1С1, тогда
А1В1С1, тогда
А1В1 = k АВ, А1С1 = k АС и В1С1 = k ВС, то получим ![]() .
.
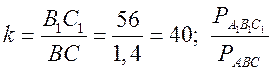 = 40.
= 40.
IV. Итоги урока.
I. ![]() АВС
АВС ![]()
![]() А1В1С1
А1В1С1 ![]()
![]() В =
В = ![]() В1 и
В1 и 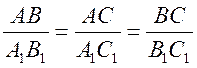 = k.
= k.
II. ![]() АВС
АВС ![]()
![]() А1В1С1
А1В1С1 ![]()
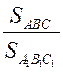 = k2.
= k2.
III. ![]() АВС
АВС ![]()
![]() А1В1С1
А1В1С1 ![]()
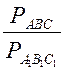 = k.
= k.
Домашнее задание: вопросы 3 и 4, с. 160; №№ 543, 546, 549.
Для желающих.
1. В трапеции АВСD (АD || ВС) АС – биссектриса угла А делит трапецию на два подобных треугольника АВС и АСD, АВ = 9 см, СD = 12 см. Найдите периметр трапеции.
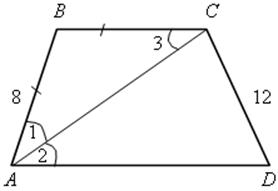
Решение
1) ![]() 2 =
2 = ![]() 3, как внутренние накрест лежащие углы при ВС || АD и секущей АС.
3, как внутренние накрест лежащие углы при ВС || АD и секущей АС.
2) ![]() АВС равнобедренный, АВ = ВС.
АВС равнобедренный, АВ = ВС.
3) ![]() АВС
АВС ![]()
![]() АСD
АСD ![]()
![]() = k; k =
= k; k = 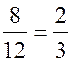 .
.
4) 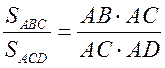 = k2;
= k2; 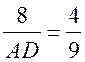 ; AD = 18.
; AD = 18.
5) РАВСD = 8 + 8 + 12 + 18 = 46 (см).
2. Прямая DЕ, параллельная стороне АС треугольника АВС, отсекает от него треугольник DВЕ, стороны которого в четыре раза меньше сторон данного треугольника. Найдите площадь треугольника АВС, если площадь трапеции АDЕС равна 30 см2.
Решение
![]() АВС
АВС ![]()
![]() DВЕ, k = 4.
DВЕ, k = 4.
Пусть SDВЕ = х, тогда SАВС = х + 30,
имеем 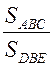 = k2;
= k2; 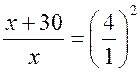 ; x + 30 = 16x; x = 2.
; x + 30 = 16x; x = 2.
SАВС = 32 (см2).