Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью - урок 2 - КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Самостоятельная работа

Вариант I

I уровень

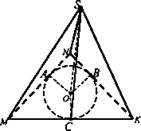
Через центр вписанной в треугольник окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.

II уровень

Из вершины равностороннего треугольника AВС восстановлен перпендикуляр AD к плоскости треугольника. Найдите расстояние от точки D до стороны ВС, если AD = 13 см. ВС = 6 см.

III уровень

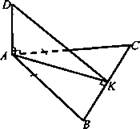
Точка М, лежащая вне плоскости данного прямого угла, удалена от вершины угла на расстояние а, а от его стороны на расстояние b. Найти расстояние от точки М до плоскости угла.

Вариант II

I уровень

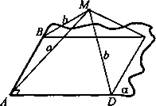
Расстояние от данной точки до плоскости треугольника равно 1,1 м, а до каждой из его сторон 6,1 м. Найти радиус окружности, вписанной в этот треугольник.

II уровень

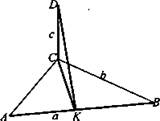
Из вершины прямого угла С треугольника AВС восстановлен перпендикуляр CD к плоскости треугольника. Найдите расстояние от точки D до гипотенузы ΔАВС, если АВ = а, ВС = b, CD = с.

III уровень

Дан равнобедренный треугольник с основанием 6 см и боковой стороной 5 см. Из центра вписанного круга восстановлен перпендикуляр к плоскости треугольника длиной 2 см. Найти расстояние от конца этого перпендикуляра до сторон треугольника.