Повторение. Перпендикулярность прямой и плоскости. Теорема о трех перпендикулярах. Угол между прямой и плоскостью - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ

Цели урока:

- повторение теоретического материала;

- обобщение навыка решения задач по данной теме;

- проверка уровня сформированных навыков при решении задач.

Ход урока

I. Проверка домашнего задания № 105, 108

II. Повторение теоретического материала

Вопросы:

1. Какие прямые в пространстве называются перпендикулярными?

2. Дайте определение перпендикулярности прямой и плоскости.

3. Сформулируйте признак перпендикулярности прямых в пространстве.

4. Сформулируйте признак перпендикулярности прямой и плоскости.

5. Что называется расстоянием от точки до плоскости?

6. Что такое наклонная, проведенная из данной точки к плоскости? Что такое проекция наклонной?

7. Сформулируйте прямую и обратную теоремы о трех перпендикулярах.

8. Сформулируйте признак перпендикулярности плоскостей.

9. Что называется углом между прямой и плоскостью?

III. Решение зада.

Задача № 158 (рис. 1).

Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости.

Найдите расстояние от точки М до прямых, содержащих стороны ромба, если АВ = 25 см, ∠BAD = 60°, ВМ = 12,5 см.

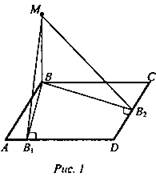
Решение: MB ⊥ (ABCD) ⇒ MB ⊥ АВ, MB ⊥ BC ⇒ MB = 12,5 см. BB1 ⊥ AD, BB2 ⊥ CD. По теореме о трех перпендикулярах МВ1 ⊥ AD, MB2 ⊥ DC. ∠A = ∠C, АВ = ВС, значит, ΔАВ1В = ΔСВ2В, ВВ1 = ВВ2 = 25 · sin60° = 12,5√3 (см).

Проекции ВВ1 и ВВ2 наклонных МВ1 и МВ2 равны, значит, равны и наклонные (Ответ: 12,5 см, 12,5 см, 25 см.)

Задача № 165. Из точки А, удаленной от плоскости γ на расстояние d, проведены к этой плоскости наклонные АВ и АС под углом 30° к плоскости. Их проекции на плоскость γ образуют угол в 120° (рис. 2).

Найдите: ВС.

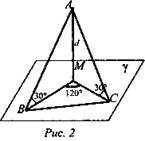
Решение: ΔАМС = ΔАМВ (по катету и острому углу). ΔВМС: по теореме косинусов (Ответ: 3d.)

IV. Самостоятельная работа (см. приложение)

Решение самостоятельной работы:

Вариант .

I уровень (рис. 3).

Решение:

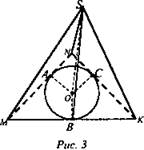
1) Точки А, В, С - точки касания сторон треугольника с окружностью. О - центр окружности, S - точка на перпендикуляре. R = ОА = ОВ = ОС;

2) По теореме о трех перпендикулярах SA ⊥ MN, ΔSOA - прямоугольный, т. e. все расстояния от точки S до сторон треугольника равны.

II уровень

Решение (рис. 4):

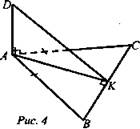
1) Проведем AK ⊥ BC, по теореме о трех перпендикулярах DK ⊥ BC, D - искомое расстояние.

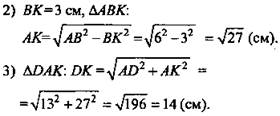(Ответ: 14 см.)

III уровень

Решение (рис. 5).

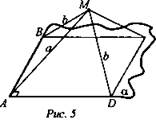
Пусть α - плоскость данного угла BAD, MB = MD - b, МА = a, MC - перпендикуляр к плоскости угла. По теореме о трех перпендикулярах ВС ⊥ АВ, DC ⊥ AD, причем ВС = CD как проекции равных наклонных. Следовательно, ABCD - квадрат. ΔDCM: (Ответ: )

Вариант II

I уровень

Решение (рис. 6):

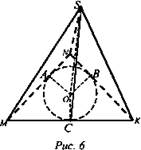
1) SO= 1,1 м; SB, SC, SA - наклонные к сторонам треугольника. АО = ВО = СО - проекции.

2) По теореме о трех перпендикулярах AO ⊥ MN, OB ⊥ NK, ОС ⊥ МК. Следовательно, О - центр вписанной окружности. из ΔSOB. (Ответ: 6 см.)

II уровен.

Решение (рис. 7):

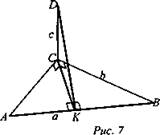
1) Проведем DС ⊥ плосксти ABC, CK ⊥ AB (высота ΔАВС) DK - наклонная;

2) По теореме о трех перпендикулярах DK ⊥ AB, следовательно, DK - искомое расстояние;

(Ответ: )

III уровен.

Решение (рис. 8):

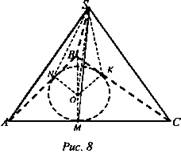
Пусть SK - искомое расстояние. К, М, N - точки касания сторон треугольника с окружностью SK = SM = SN. r = ОК, ОК ⊥ ВС. По теореме о трех перпендикулярах SK ⊥ BC. ΔSOK - прямоугольный. где р - полупериметр. (Ответ: 2,5 см.)

V. Подведение итогов

- Как найти угол между прямой и плоскостью?

Домашнее задание

П. 20 учебника, № 143; 149.