Поурочные разработки по Геометрии 11 класс
Объем конуса - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ
Цели урока:
- вывести формулу объема конуса с помощью определенного интеграла;
- рассмотреть следствие из теоремы, в котором выводится формула объема усеченного конуса.
- показать применение полученных формул при решении типовых задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
Теоретический опрос.
Повторить понятия конуса n усеченного конуса.
1. Рассмотрим окружность L с центром в точке О и прямую ОР, перпендикулярную плоскость α. Каждую точку окружности соединим отрезком с точкой Р. Поверхность, образованная этими отрезками, называется... (рис. 1).
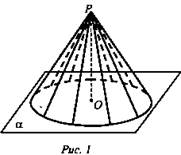
2. Тело, ограниченное конической поверхностью и кругом, называется:
а) Цилиндром.
б) Конусом.
в) Пирамидой.
3. Установите соответствие между элементами конуса (рис. 2).
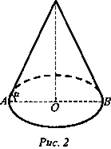
a) SO .
б) SA, SB -
b) S -
г) ОА -
д) ∠α.
4. Конус может быть получен вращением прямоугольного треугольника вокруг (рис. 3):
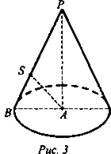
а) гипотенузы РВ;
б) катета РА;
в) отрезка AS.
5. Выберите чертеж с сечением, перпендикулярным оси конуса (рис. 3 а), б), в)).
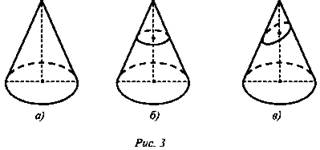
6. Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет собой конус, а другая называется усеченным конусом.
7. Установите соответствие (рис. 4).
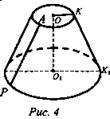
а) ОК .
6) О1К1 .
в) АР -
г) O1O -
8. Вращением какой трапеции вокруг ее боковой стороны может быть получен усеченный конус?
а) любой;
б) прямоугольной;
в) равнобедренной.
Повторить вопросы планиметрии.
1) Записать формулу для вычисления площади круга (S = πR2).
2) Дать определение подобия фигур.
3) Сформулировать признаки подобия треугольников.
Повторить конспект урока № 39.
В прямоугольной системе координат на плоскости рассмотрим криволинейную трапецию, ограниченную графиком непрерывной неотрицательной функции f(x), осью абсцисс и прямыми х = а и х = b (а < b). Рассмотрим тело, полученное вращением вокруг оси абсцисс криволинейной трапецией (рис. 5).
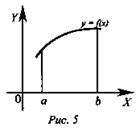
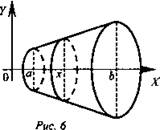
Очевидно, что сечение этого тела плоскостью, проходящей через точку с абсциссой х ∈ [а; b] и перпендикулярной оси Ох, есть круг (или точка) радиуса f(x). Следовательно, площадь S(x) этого сечения равна S(x) = πf2(x), а объем рассматриваемого тела вращения вычисляется по формуле ![]() (рис. 6).
(рис. 6).
III. Изучение нового материал.
Теорема. Объем конуса равен одной трети произведения площади основания на высоту (рис. 7).
![]()
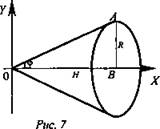
Доказательство: Данный конус можно рассматривать как тело, полученное вращением прямоугольного треугольника с вершиной в точках О(0; 0), В(Н; 0), А(Н; R) вокруг оси Ох. Уравнение прямой ОА имеет вид: у = kх, где ![]() Треугольник ОАВ является частным видом криволинейной трапеции, которая ограничена осью абсцисс, графиком функции
Треугольник ОАВ является частным видом криволинейной трапеции, которая ограничена осью абсцисс, графиком функции ![]() и прямой х = Н.
и прямой х = Н.
Поэтому объем конуса можно найти с помощью формулы (1), то есть 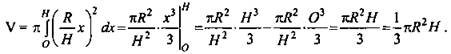 Площадь основания конуса равна S = πR2, поэтому
Площадь основания конуса равна S = πR2, поэтому ![]() Теорема доказана.
Теорема доказана.
Следствие. Объем усеченного конуса с радиусами оснований r и R и высотой H вычисляется по формуле ![]()
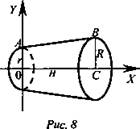
Доказательство (рис. 8): Усеченный конус можно получить вращением вокруг оси Ох трапеции ОАВС. Прямая АВ проходит через точки (0; r) и (Н; R), поэтому она имеет уравнение ![]() (уравнение прямой вывести самостоятельно). Используя формулу (1), получим
(уравнение прямой вывести самостоятельно). Используя формулу (1), получим ![]()
Для вычисления интеграла сделаем замену ![]() Очевидно, когда х изменяется в пределах от 0 до H, перемещаясь, изменяется от r до R, и поэтому
Очевидно, когда х изменяется в пределах от 0 до H, перемещаясь, изменяется от r до R, и поэтому
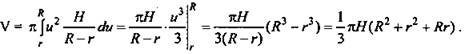
Следствие доказано.
Формулу ![]() доказать самостоятельно.
доказать самостоятельно.
IV. Закрепление изученного
1. Решить (устно) задачи с целью закрепления формул для вычисления объемов конуса и усеченного конуса.
№ 1. Вычислите объем конуса, если его высота 6 см, а площадь основания 42 см2. (Ответ: 84 см3.)
№ 2. Объем конуса с радиусом основания 4 м и высотой 6 м равен: (Ответ: 32π м3.)
№ 3. Найдите площадь основания конуса, если его объем равен 256 см3, а высота 4 м. (Ответ: 252 см2.)
№ 4. Вычислите объем усеченного конуса, высота которого 3 см, а площадь оснований 16 см2 и 4 см2. (Ответ: 32 см3.)
№ 5. Вычислите объем усеченного конуса, если радиусы его оснований равны 3 см и 9 см, а высота 6 см. (Ответ: 234π см3.)
2. Решить в рабочих тетрадях и на доске задачи:
№ 1. Образующая конус l составляет с плоскостью основания угол α. Найдите объем конуса.
№ 2. Радиусы оснований усеченного конуса R и r; образующая наклонена к плоскости основания под углом 45°. Найдите объем конуса.
№ 3. Длина образующей конуса равна l, а длина окружности основания С. Найдите объем конуса.
Решение задач.
№ 1. (рис. 9).
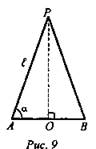
ΔРАВ - осевое сечение конуса, РА = РВ = l, РО - высота, ![]() Из ΔAPO (∠O = 90°):
Из ΔAPO (∠O = 90°): ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 2. (рис. 10).
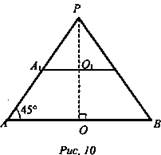
(R > r)
I способ:
Дополнить усеченный конус до полного и тогда ![]() где
где ![]()
![]() Из ΔAPO (∠O = 90°): ∠APO = 45°, значит, РО = AO = R. Из ΔА1PO1 (∠O = 90°): ∠A1 = 45°, значит,
Из ΔAPO (∠O = 90°): ∠APO = 45°, значит, РО = AO = R. Из ΔА1PO1 (∠O = 90°): ∠A1 = 45°, значит, ![]()
![]()
II способ:

Рассмотреть трапецию AA1O1О (рис. 11).
Д.П.: ![]() Из ΔАА1А2 (∠A2 = 90°): ∠AA1A2 = 45°, значит,
Из ΔАА1А2 (∠A2 = 90°): ∠AA1A2 = 45°, значит, ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 3. (рис. 12).
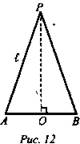
ΔAPB – осевое сечение конуса. ![]()
![]() Из ΔAPO(∠O = 90°): по теореме Пифагора
Из ΔAPO(∠O = 90°): по теореме Пифагора ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
V. Подведение итогов
- Как найти объем усеченного конуса?
- Отметим, что формула объема усеченного конуса такая же, как и формула объема усеченной пирамиды.
Записать домашнее задание.
П. 70. № 701, 704, 709.
![]() - вывести самостоятельно.
- вывести самостоятельно.
![]() - вывести самостоятельно.
- вывести самостоятельно.
Дополнительная задача: Равносторонний треугольник вращается вокруг своей стороны а. Найдите объем полученного тела вращения.