Объем пирамиды - урок 3 - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ

Цель урока:

- выработать навыки решения типовых задач на применение формул объемов пирамиды и усеченной пирамиды.

Ход урока

I. Проверка домашнего задания

(на доске № 697)

Задача № 697. Дано: АВСА1В1С1 - правильная усеченная пирамида. АВ = а, А1В1 = 0,5а. ММ1 ⊥ ВС, ММ1 = а (рис. 1).

Найти: Vус.пир. - ?

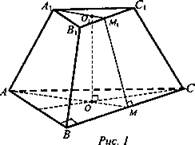
Решение:

1) Рассмотрим ΔАВС, найдем

2) ΔА1В1С1, найдем A1М1 (A1М1 ⊥ В1С1).

3)

4) Рассмотрим прямоугольную трапецию ОО1М1М (рис 1 a)):

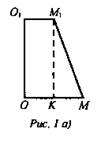
Из ΔКМ1М: ∠K = 90°, по теореме Пифагора.

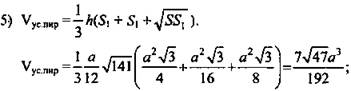
(Ответ: )

II. Решение задач

1. Дано: A1A2A3A4 - трапеция, А1А4 = А3А2, О - центр окружности, вписанной в трапецию SO ⊥ (А1А2А3), А1А4 = а1 (рис. 2).

Найти: Vпир. - ?

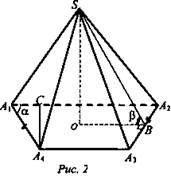
Решение:

1) Проведем A4C ⊥ A1A2. Рассмотрим ΔА1СA4. ∠С = 90°, А1А4 = а, тогда А1С = h = asinα,

2) H = SO = OBtgβ = 0,5a sinαtgβ.

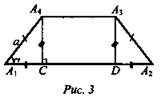
3) Рассмотрим равнобедренную трапецию A1A2A3A4, найдем ее площадь. Н = А4С = asinα. Пусть CD = x, тогда (рис. 3) А1С = acosα, подставим в формулу, С одной стороны, площадь многоугольника можно найти через периметр и радиус вписанной окружности. тогда Уравняем правые части, После упрощения получим х = а - acosα. Итак, площадь основания равна

4) (Ответ: )

III. Проверочная самостоятельная работа (разноуровневая) (см. приложение.

Ответы:

Вариант А1 192 см3. Вариант Б1 343 см3. Вариант B1

Вариант A2 360 см3. Вариант Б2 320 см3. Вариант B2

Решение проверочной самостоятельной работы

Вариант A1

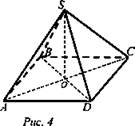
Решение:

1) AS = BS = CS = DS, значит, АО = ВО = СО = DO.

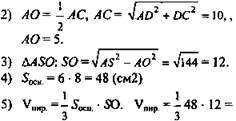192 см3. (Ответ: 192 см3.)

Вариант А2

Решение:

360 см3. (Ответ: 360 см3.)

Вариант Б1

Решение:

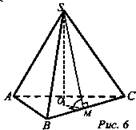
1) ∠SMO = 45°, точка О - центр вписанной в основание окружности, ОМ = r, ОМ ⊥ ВС.

2) формула Герона. с др. стороны

3) ΔSOM - равнобедренный, SO = ОМ = 7 см.

4) (Ответ: 343 см3..

Вариант Б2

Решение:

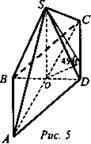
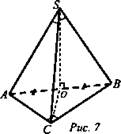
1) Так как ∠ASO = ∠BSO = ∠CSO = 45°, то ∠SAO = ∠SBO = ∠SCO; тогда AО = OB = ОС = R.

2) ОА = OB, точка О - центр окружности, описанной около основания.

(Ответ: 320 см3.)

Вариант В1

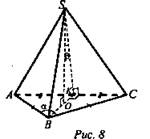
Решение:

1) Пусть BC = а,

2) с другой стороны Приравниваем,

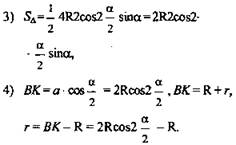
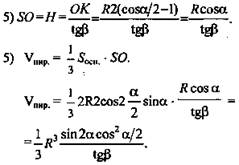
(Ответ: )

Вариант В2

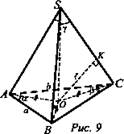
Решение:

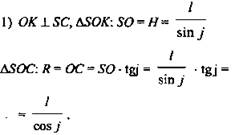
2) Составим равенство из формул для вычисления площадей треугольника.

3)

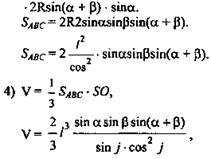
(Ответ: ).

Домашнее задание

Обменяться вариантами самостоятельной работы.