Поурочные разработки по Геометрии 11 класс

Сфера. Уравнение сферы - Сфера - ЦИЛИНДР, КОНУС И ШАР

Цели урока:

- ввести понятие сферы, шара и их элементов;

- вывести уравнение сферы в заданной прямоугольной системе координат;

- формировать навык решения задач по данной теме.

Ход урока

I. Организационный момент

II. Самостоятельная работа (см. приложение).

Самостоятельная работа записывается в домашних тетрадях.

Решение:

I уровень

Вариант I

Дано: усеченный конус, O1С = 3 см, OD = 6 см, OO1 = 4 см (рис. 1).

Найти: Sсеч., Sбок.

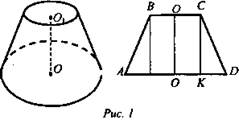
Решение: Осевым сечением усеченного конуса является равнобедренная трапеция. ΔCKD - прямоугольный, по теореме Пифагора (Ответ: Sсеч. = 36 cм2, Sбок. = 45π см2.)

Вариант II

Дано: усеченный конус, OD = 7 см, CD = 5 см, ОО1 = 4 см (рис. 2).

Найти: Sсеч., Sбок.

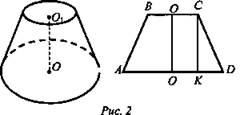
Решение: Осевым сечением усеченного конуса является равнобедренная трапеция. ΔCKD - прямоугольный, по теореме Пифагора (Ответ: Sсеч. = 44 cм2, Sбок. = 55π см2.)

II уровень

Вариант I

Дано: усеченный конус, АС = 40 см, AC ⊥ CD, CD = 30 см (рис. 3).

Найти: Sсеч., Sr.

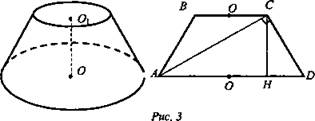
Решение: Сечение усеченного конуса является равнобедренная трапеция ΔADC - прямоугольный, по теореме Пифагора Так как СН - высота прямоугольного треугольника, то СН2 = АН · HD. ΔCHD - прямоугольный.

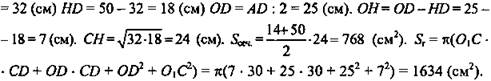
(Ответ: Sсеч. = 768 см2, Sr = 1634π см2.)

Вариант II

Дано: Усеченный конус, O1С = 1 дм, OD = 7 дм, BD ⊥ AС (рис. 4).

Найти: Sсеч., Sr.

Решение: Осевым сечением усеченного конуса является равнобедренная трапеция. ΔВМС - прямоугольный и равнобедренный: ΔAMD — прямоугольный и равнобедренный: ΔMO1C- прямоугольный: ΔAОМ - прямоугольный: ΔСHD - прямоугольный:

(Ответ: Sсеч.= 64 дм2, Sr = 130π дм2.)

III уровень

Вариант I

Дано: усеченный конус O1С = 16 см, OD = 25 см. Окружность, вписанная в сечение (осевое) (рис. 5).

Найти: Sr.

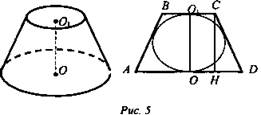
Решение: Осевым сечением усеченного конуса является равнобедренная трапеция. Так как в трапецию вписана окружность, то O1С = CF = 16 (см) и OD = DF = 25 (см) (как отрезки касательных к окружности, проведенных из одной точки). ΔCHD - прямоугольный: (Ответ: Sr = 2562π см2.)

Вариант II

Дано: усеченный конус, AF= 35 см, FC = 10 см, CD = 39 см (рис. 6).

Найти: Sr.

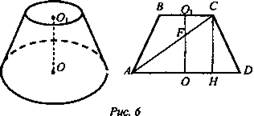
Решение: . ΔAOF ∞ ΔAHC (по двум углам): ΔАСН — прямоугольный: по теореме Пифагора ΔCHD - прямоугольный:

(Ответ: Sr = 1530π см2.)

III. Изучение нового материала

Вспомните определение окружности.

Окружность - множество точек плоскости, равноудаленных от данной точки.

Дайте определение сферы.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

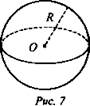
Данная точка О называется центром сферы, а данное расстояние - радиусом сферы. Обозначается R. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Диаметр сферы равен 2R. Вспомните определение круга.

Круг - это часть плоскости, ограниченная окружностью. Дайте определение шара:

Тело, ограниченное сферой, называется шаром. Существует и другое определение шара:

Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

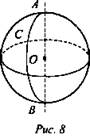
Сфера может быть получена вращением полуокружности вокруг ее диаметра, а шар - вращением полукруга вокруг его диаметра.

Сфера получена вращением полуокружности АСВ вокруг диаметра АВ.

Прежде чем вывести уравнение сферы познакомимся с понятием уравнения поверхности в пространстве.

Введем прямоугольную систему координат Oxyz и некоторую поверхность F.

Уравнение с тремя переменными х, у, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Выведите самостоятельно уравнение сферы радиуса R с центром С(х0, у0, z0), используя формулу для вычисления расстояния между двумя точками с заданными координатами.

Найдите расстояние от произвольной точки М(х, у, z) до С(х0, у0, z0) (рис. 9).

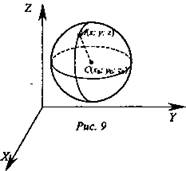
Если точка М лежит на сфере, то MC = R.

так, как любая точка сферы, то уравнение сферы

Если же точка М не лежит на данной сфере, то МС ≠ R, т.е. координаты точки М не удовлетворяют уравнению Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С (х0, у0, z0) имеет вид

IV. Закрепление изученного материала

№ 573 а). Дано: А и В лежат на сфере, О ∉ АВ, АМ = МВ (рис. 10).

Доказать: ОМ ⊥ AB.

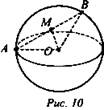
Доказательство: ΔAОВ - равнобедренный (АО = ОВ = R), АМ = MB (по условию), значит ОМ - медиана ΔАОВ. Так как медиана в равнобедренном треугольнике, опущенная к основанию, является высотой, то ОМ ⊥ AB.

№ 574 а) (используется тот же чертеж) решить самостоятельно.

Дано: А и В лежат на сфере, R = 50 см, АВ = 40 см. АМ = MB.

Найти: ОМ.

Так как ОМ ⊥ AB (смотрите предыдущую задачу), то ΔАМО - прямоугольный. По теореме Пифагора