Поурочные разработки по Геометрии 11 класс
Усеченный конус - Конус - ЦИЛИНДР, КОНУС И ШАР
Цели урока:
- ввести понятие усеченного конуса;
- вывести формулы для вычисления площади боковой и полной поверхности усеченного конуса;
- разобрать задачи по данной теме.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний
1) Проверка домашнего задания. У доски два человека делают чертеж и пишут решение № 562 и 563.
2) Третий ученик и класс решают задачу по планиметрии: Найти боковую сторону равнобедренной трапеции, если ее основания 6 см и 12 см, а высота 4 см.
Дано: ABCD - равнобокая трапеция, ВС || AD; ВС = 6 см, AD = 12 см. ВН = 4 см - высота (рис. 1).
Найти: CD.
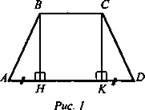
Решение: ВН = СК - высоты, BA = CD, ΔАВН = ΔDCK (по катету и гипотенузе) АН = KD = (AD - ВС) : 2. АН = KD = 3 см, из ΔDCK, ![]() (Ответ: CD = 5 см.)
(Ответ: CD = 5 см.)
3) Сравните домашние задачи и решение на доске. Какие еще есть вопросы по домашней работе?
III. Изучение новой темы
Сегодня мы познакомимся еще с одной геометрической фигурой и ее свойствами. Запишите тему урока «Усеченный конус». Посмотрите на модель конуса, я провожу секущую плоскость, перпендикулярно оси конуса. Эта плоскость, разбивает наш конус на две части. Одна часть - это меньший конус - подобный данному, а другая называется усеченным конусом. Посмотрите на рис. 145 с. 125 учебника. А теперь изучите рисунок усеченного конуса (рис. 147, с. 126).
А теперь делаем рисунок в тетрадь и работаем с ним (рис. 2).

1. Основания усеченного конуса (2 круга).
2. Высота усеченного конуса O1O (расстояние между плоскостями оснований).
3. Ось усеченного конуса b.
4. Особое сечение усеченного конуса (равнобокая трапеция с основаниями 2R и 2R1, где R и R1 радиусы оснований усеченного конуса) ABCD — трапеция.
5. Образующие усеченного конуса равны l (это отрезки, соединяющие соответственные точки окружностей оснований, например AD, ВС). Если мы вспомним задачу, которую решали в начале урока, то исходя из l2 = Н2 + (R - R1)2 решим устно № 567.
6. Боковая поверхность усеченного конуса (часть конической поверхности, ограничивающая усеченный конус). ![]()
![]() так как ∠O = ∠O1 = 90° и ∠S - общий,
так как ∠O = ∠O1 = 90° и ∠S - общий, ![]() или
или ![]()
![]()
7. Полная поверхность усеченного конуса ![]()
8. Усеченный конус получается также вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основанием (посмотрите рис. 148 на с. 126).
IV. Закрепление изученного материал.
Задача № 572.
![]() Расход краски:
Расход краски: ![]() (Ответ: 2,55π ≈ 8,011 кг.)
(Ответ: 2,55π ≈ 8,011 кг.)
V. Подведение итогов
- Итак, сегодня на уроке мы узнали о свойствах усеченного конуса и на примере убедились в практической значимости теоретических знаний геометрии.
- Какую форму имеет осевое сечение усеченного конуса? (Ответ: Осевое сечение усеченного конуса является равнобедренной трапецией.)
Домашнее задание
П. 57.1 уровень № 568, 569, 571 и II уровню добавляем № 618.
Задача № 618.
Дано: усеченный конус, ABDC - осевое сечение, ВС ⊥ AD; SABCD = 36 дм2 (рис. 3).
а = 40 см - одно основание.
Найти: Sб. и Sп. усеченного конуса.
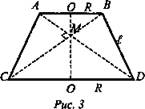
Решение:
1. Если диагонали равнобокой трапеции взаимно перпендикулярны, то SABCD = h2, тогда
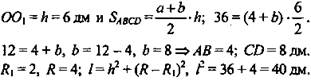
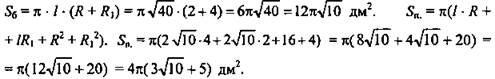
(Ответ: ![]() )
)