Урок 23. Контрольная работа № 1 - Контрольные и самостоятельные работы - ПРИЛОЖЕНИЯ

I уровень

Вариант I

1. Даны параллельные плоскости α и β. Через точки А и В плоскости проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1. Найдите А1В1, если АВ = 5 см.

2. Верно, что плоскости параллельны, если прямая, лежащая в одной плоскости, параллельна другой плоскости?

3. Две плоскости параллельны между собой. Из точки М, не лежащей ни в одной из этих плоскостей, ни между плоскостями, проведены две прямые, пересекающие эти плоскости соответственно в точках А1 и А2, В1 и В2. Известно, что МА1 = 4 см, В1В2 = 9 см, A1A2 = МВ1. Найдите МА2 и МВ2.

Вариант II

1. Отрезки АВ и CD параллельных прямых заключены между параллельными плоскостями. Найдите АВ, если CD = 3 см.

2. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

3. Из точки О, лежащей вне двух параллельных плоскостей α и β, проведены три луча, пересекающие плоскости α и β соответственно в точках А, В, С и А1, В1, С1 (ОА < ОА1). Найдите периметр А1В1С1, если ОА = m, АА1 = n, АВ = 6, ВС = а.

II уровень

Вариант I

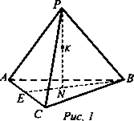
1. Построить сечение, проходящее через линии и точки, выделенные на чертеже (рис. 1).

2. Ребро куба ABCDA1B1C1D1 равно 2 см. Найдите расстояние между прямыми АВ и B1D.

3. Докажите, что линии пересечения двух пар параллельных плоскостей параллельны.

Вариант II

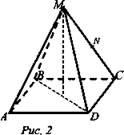
1. Построить сечение, проходящее через линии и точки, выделенные на чертеже (рис. 2).

2. Дан прямой параллелепипед ABCDA1B1C1D1, основанием которого является ромб АВCD, угол BAD = 30°, АВ = 18, ВВ1 = 12. Найти площадь AB1C1D.

3. Непараллельные отрезки АВ и CD лежат соответственно в параллельных плоскостях α и β. Что можно сказать о взаимном расположении прямых АС и ВО?

III уровень

Вариант I

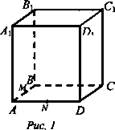
1. Построить сечение, проходящее через точки, выделенные на рисунке (рис. 1).

2. Между двумя параллельными плоскостями заключены перпендикуляр длиной 3 м и наклонная, равная 5 м. Расстояние между концами их (в каждой плоскости) равно 4 м. Найдите расстояние между серединами перпендикуляра и наклонной.

Вариант II

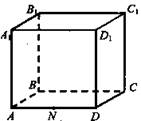
1. Построить сечение, проходящее через точки, выделенные на рисунке (рис. 2).

2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором AD = а, АВ = b, АА1 = с. Найдите длины отрезков D1P и CN, где Р - середина отрезков В1С, N - середина отрезка А1В1.