Заключительный урок-беседа по курсу геометрии - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ

Цели урока:

1) формировать и развивать эвристическое мышление;

2) показать какую роль играет геометрия в развитии общества;

3) систематизировать знания в истории развития геометрии.

Ход урока

I. Вступительное слово учителя

(на экране диапроектора слайд № 1)

Геометрия - одна из самых, а может, самая древняя наука, ее возраст исчисляется тысячелетиями. В геометрии много формул, фигур, теорем, задач, аксиом. Это своего рода «автографы», оставленные учеными своим потомкам. Они вечны, так как на них запечатлены великие идеи, не проходящие идеи. Давайте совершим маленькое путешествие во времени.

1. Остановка «Древний Египет»

Ученик: Древний Египет считается первым государством, оставившим самые ранние математические тексты. Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян. Геродот писал: «Египетские жрецы говорили, что царь разделил землю между всеми египтянами, дав каждому по равному прямоугольному участку; из этого он создал себе доходы, приказав ежегодно вносить налог. Если же река отнимала что-нибудь, то царь посылал людей, которые должны измерить участок и уменьшить налог». Первой книгой, содержащей геометрические задачи, считается папирус Райнда, который датируется IXX веком до нашей эры. Что умели древние египтяне:

1) Умели точно находить площадь поля прямоугольной, треугольной, трапециевидной формы.

2) Умели строить прямоугольный треугольник при помощи веревки, разделенной узлами на 12 равных частей.

3) Знали, что отношение длины окружности к диаметру - число постоянное, приближенное значение этого числа - π.

4) Среди пространственных тел самым египетским можно считать пирамиду, ведь именно такую форму имеют знаменитые усыпальницы фараонов, хотя довольно близко они знакомы с кубом, параллелепипедом, призмой и цилиндром, умели вычислять объем этих фигур.

5) Умели вычислять объем усеченной пирамиды, в основании которых квадраты по формуле

2. Остановка «Древняя Греция»

Ученик: Пожалуй, дату появления геометрии, как науки, можно определить довольно точно - VI век до нашей эры.

Древнегреческий ученый Фалес Милетский считается одним из первых геометров. Он был причислен к семи мудрецам древности, среди которых он первый. Фалес решил следующие задачи.

1) Предложил способ определения расстояния до корабля на море.

2) Вычислил высоту египетской пирамиды Хеопса по длине отбрасываемой тени.

3) Доказал равенство углов при основании равнобедренного треугольника.

4) Ввел понятие движения, в частности поворота.

5) Доказал второй признак равенства треугольников и впервые применял его в задаче.

6) Теорема Фалеса о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.

Пример: задача об измерении высоты пирамиды.

Однажды, отправившись по торговым делам в Египет, он задержался там на несколько лет. Случилось так, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить. Фалес смог легко справиться с задачей.

Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды. Фараон и его приближенные изумились такому достаточно простому решению.

3. Остановка «Школа Евклида»

Евклид Александрийский. О нем известно очень мало. Вот два эпизода связанные с его именем.

Рассказывают, что египетский царь Птолемей I пожелал лично познакомиться с прославленным математиком и с его не менее известными сочинениями. Он милостиво выслушал доказательство двух теорем, но в начале третьей с ужасом воскликнул: «Неужели нет других путей для того, чтобы понять эти вещи?» На это Евклид с достоинством ответил: «Нет, в математике даже для царей нет других путей!» Евклид является непревзойденным систематизатором, педагогом и популяризатором науки. Своими учебниками (то есть книгами «Начала») он охватил всю элементарную математику той эпохи. «Начала» состоят из 13 книг. Первые четыре посвящены геометрии на плоскости. Каждую книгу он начинает с пяти аксиом и постулатов. Вспомните их! В первой книге излагается планиметрия прямолинейных фигур: устанавливаются их свойства, заканчивается прямой и обратной теоремой Пифагора. Во второй книге излагается основы геометрической алгебры. Третья книга посвящена свойствам круга, в четвертой строятся правильные n-угольники при n = 3, 4, 5, 6, 10, 15. Исключительное изящное построение правильного 15-угольника принадлежит самому Евклиду. 11 книга посвящена стереометрии. Она содержит основные теоремы о прямых и плоскостях в трехмерном пространстве, задачи на построение, например как опустить перпендикуляр из данной точки на данную плоскость. 12 книга посвящена решению задачи о квадратуре круга. 13 книга излагает учение о правильных многогранниках. В целом творение Евклида величественно. Созданная им система просуществовала более двух тысяч лет. Вплоть до XX века геометрию преподавали по популярным переводам этой книги. Но последующие математики не во всем соглашались с системой аксиом и определений и пытались ее улучшить. Некоторые оказались ненужные, например, что прямые углы равны. Это очевидно из других аксиом. Особенное неудовлетворение всегда вызывал пятый постулат, утверждавший: что через любую точку плоскости можно провести только одну прямую параллельную данной. Многие считали ее теоремой и пытались ее неудачно доказать.

Учитель: Всегда ли это верно? Ответить на этот вопрос смогли лишь через две тысячи лет.

4. Остановка «Геометрия Лобачевского»

Ученик: В 1826 году великий русский математик Николай Иванович Лобачевский поставил точку в проблеме пятого постулата.

Вместо него он принял допущение, согласно которому в плоскости можно построить, по крайней мере, две прямые, не пересекающиеся с а. Дальнейшие его рассуждения привели его к новой безупречной геометрической системе, называемой сейчас геометрией Лобачевского. В его геометрии сумма углов треугольника меньше 180°, в ней нет подобных фигур. В ней существуют треугольники с попарно параллельными сторонами. Все это непривычно и необычно, с || а; b || а.

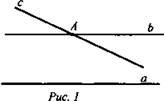
Но геометрия Лобачевского - геометрия Вселенной, геометрия бесконечного пространства, таящего в себе множество нераскрытых тайн.

Но несмотря на то, что возраст геометрии исчисляется тысячелетиями, геометрия и сейчас продолжает бурно развиваться.

Учитель: Геометрия - молодая наука. Ее уникальность в том, что некоторые самые современные достижения геометрической науки доступны школьникам. Вот одно из них.

Ученик: Рассмотрим несколько задач на пространственное воображение, изображение и соображение...

1) Может ли рисунок служить изображением многогранника с тремя четырехугольными гранями и двумя треугольными? (рис. 2).

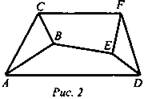
Ответ: Нет. Прямые АВ, BE, CF должны пересекаться в одной точке.

2) На рисунке изображена пирамида, в которой проведены два отрезка, соединяющие точки на противоположных ребрах. Можно ли определить по рисунку, пересекаются эти отрезки или нет?

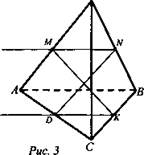
Ответ: Можно. Отрезки MN и DK пересекаются, то есть лежат в одной плоскости, когда точка пересечения прямых, которым отрезки принадлежат, лежит на прямой АВ, либо они параллельны.

3) Каждое ребро тетраэдра поделили на три равные части и через точки деления провели плоскости, параллельные граням. На сколько и каких частей они разрезают тетраэдр.

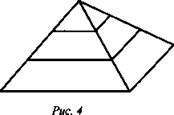
Ответ: На 15 частей: 11 тетраэдров, втрое меньших, и 4 правильных октаэдра.

Учитель: Любая решенная в геометрии проблема порождает ряд новых. Что будет дальше, мы не знаем. Быть может, сейчас седой ученый совершает доказательство очередной теоремы. А может быть, это кто-нибудь из вас!

II. Подведение итогов