Поурочные разработки по геометрии 10 класс
Повторение. Векторы в пространстве, их применение к решению задач - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ
Цели урока:
1) повторение и обобщение знаний по теме;
2) совершенствование навыков построения чертежей;
3) развитие логического мышления, пространственного воображения.
Ход урока
I. Организационный момент
II. Повторение теоретического материала
а) Примерные вопросы для повторения (желательно, чтобы учащиеся были ознакомлены с ними заранее).
Опрос проводится в форме «Продолжите фразу!»
Например, учитель начинает: «Два вектора называются коллинеарными, если...», ученик продолжает: «...они лежат на одной прямой или на параллельных прямых» или даёт какое-либо свое определение. Спорные ответы обсуждаются.
Что называется вектором? Нулевым вектором? Длиной вектора?
Чему равна длина нулевого вектора? Какие векторы называются кол- линеарными? Сонаправленными? Противоположно направленными? Какие векторы называются равными? Сколько векторов, равных данному, можно отложить от данной точки?
- Что называется суммой векторов ![]()
- Правило треугольника. Свойства сложения.
- Правило параллелограмма. Правило многогранника.
- Какие векторы называются противоположными?
- Что называется произведением ненулевого вектора на число?
- Что называется произведением нулевого вектора на число?
- Свойства умножения вектора на число.
- Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарные; б) любые два коллинеарных вектора сонаправлены; в) любые два равных вектора коллинеарные;
- Признак компланарности векторов.
- Компланарны ли векторы: а) а, b, 2а и 3b; б) а, b, а + b, а – b?
- Известно, что векторы а, b и с компланарны. Компланарны ли векторы а) а, 2b, 3 с; б) а + b, а + 2с, 2b - 3с?
- Точки А, В и С лежат на окружности, а точка О не лежит в плоскости этой окружности. Могут ли ОА, ОВ и ОС быть компланарными?
III. Работа по готовым чертежам
В целях экономии времени необходимо чертежи на доске выполнить заранее.
Их могут выполнить 3 ученика во время фронтальной работы с классом по вопросам для повторения.
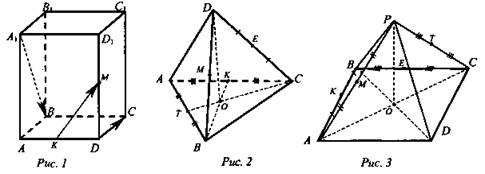
1. В прямом параллелепипеде ABCDA1B1C1D1 точки К и М- середины ребер AD и DD1 соответственно. Запишите векторы с началом и концом в вершинах параллелепипеда, которые:
а) противоположно направлены вектору ![]()
б) сонаправлены с вектором ![]()
в) имеют длину, равную длине вектора ![]()
2. В правильной треугольной пирамиде DABC точки Е, М, Т и К - середины соответственно ребер DC, DB, ВА и АС.
а) Перечислите пары противоположно направленных векторов, не лежащих на одной прямой и с началом и концом в точках Е, М, Т и К.
б) Перечислите пары равных векторов с началом и концом в точках Е, М, Т и К.
в) Перечислите векторы, имеющие равные длины, с концами в точках Е, М, Т и К.
3. В правильной четырехугольной пирамиде PABCD точки К, М, Т и Е - середины соответственно ребер АВ, РА, PC и ВС.
1) Перечислите пары сонаправленных векторов с концами в точках К, М, Т, Е.
2) Перечислите пары равных векторов с концами в точках К, М, Т и Е.
3) Перечислите векторы, имеющие равные длины, с концами в точках К, М, Т и Е.
IV. Геометрический диктант
(Выполняется на отдельных листочках, которые сдаются на проверку.)
1. Нарисуйте параллелепипед ABCDA1B1C1D1.
2. Найдите вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов ![]()
![]()
3. Найдите вектор, равный ![]()
4. Представьте вектор ![]() в виде разности двух векторов, один из которых вектор
в виде разности двух векторов, один из которых вектор ![]() [вектор
[вектор ![]() ].
].
5. Упростите выражение: MN - PQ - NM + РТ + RQ + TR; ![]()
6. Упростите выражение: ![]()
![]()
V. Решение задач
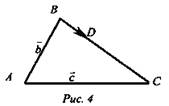
№ 1. Дан треугольник ABC. ![]() Выразите вектор
Выразите вектор ![]() через векторы
через векторы ![]() (рис. 4).
(рис. 4).
Решение: ![]()
![]() (Ответ: BD =
(Ответ: BD = ![]() )
)
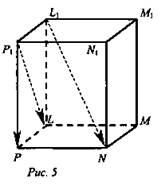
№ 2. Дан параллелепипед PLMNP1L1M1N1. Разложите вектор ![]() по векторам
по векторам ![]() и
и ![]() (рис. 5).
(рис. 5).
Решение: ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 3. Длина ребра куба ABCDA1B1C1D1 равна а. Вычислите скалярные произведения: ![]() (рис. 6).
(рис. 6).
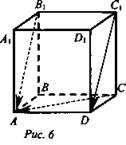
Решение:
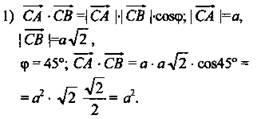
![]() (Ответ: 1) a2; 2) 2a2.)
(Ответ: 1) a2; 2) 2a2.)
Домашнее задание
I уровень
№ 1. Дан параллелограмм ABCD. ![]()
![]() Выразите вектор
Выразите вектор ![]() через векторы
через векторы ![]()
№ 2. Дан параллелепипед ABCDA1B1C1D1, ![]() Разложите вектор
Разложите вектор ![]() по векторам
по векторам ![]() если М = [АС] ∩ [BD].
если М = [АС] ∩ [BD].
№ 3. На стороне АВ треугольника ABC взята такая точка М, что |АM| : |МВ| = 1 : 1. Вычислите |МС|, если |АС| = а, |ВС| = 2а, АСВ = 60°.
№ 4. Вычислите угол между векторами ![]() где
где ![]() - единичные взаимно перпендикулярные векторы.
- единичные взаимно перпендикулярные векторы.
II уровень
№ 1. Дан параллелограмм KLMN. ![]()
![]() Выразите вектор
Выразите вектор ![]() через векторы
через векторы ![]()
№ 2. Дан тетраэдр ABCD, ![]()
![]() Выразите вектор
Выразите вектор ![]() через векторы
через векторы ![]()
№ 3. Точка К - середина стороны треугольника DEF. Вычислите расстояние |FK|, если |DF| = m, |FE| = m√2, DFE = 135°.
№ 4. Вычислите угол между векторами ![]() где
где ![]() и
и ![]() - единичные взаимно перпендикулярные векторы.
- единичные взаимно перпендикулярные векторы.
Ответы к домашнему заданию:
|
|