Поурочные разработки по геометрии 10 класс
Понятие векторов. Равенство векторов - ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ - ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цели урока:
1) ввести определение вектора в пространстве и равенства векторов;
2) рассмотреть связанные с этими понятиями обозначения.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока
II. Актуализация знаний учащихся
1. Анализ контрольной работы. Подвести итоги контрольной работы. Анализ наиболее часто встречающихся ошибок.
2. Подготовка к восприятию нового материала.
Понятие вектора является одним из наиболее основных в математике, объединяющим такие ее разделы, как геометрия, алгебра, математический анализ. Оно имеет большое прикладное значение, так как многие физические величины (сила, скорость и другие) характеризуются не только величиной, но и направлением, то есть являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин (векторы напряженности электрического поля, вектор магнитной индукции).
В планиметрии мы изучали векторы на плоскости. Здесь мы рассмотрим векторы в пространстве. Их определение и свойства аналогичны определению и свойствам векторов на плоскости.
III. Изучение нового материала
1. Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется вектором.
Ввести обозначение вектора, его длины, понятие нулевого вектора. ![]()
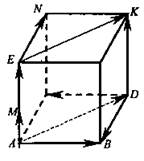
2. Ввести определения коллинеарных векторов, сонаправленных и противоположно направленных векторов. Ввести обозначения ![]()
Обратить внимание, что нулевой вектор сонаправлен любому вектору. На доске рисунок. Найти сонаправленные векторы.
Сонаправленные: ![]()
Противоположно направленные: ![]()
3. Ввести определение равных векторов: ![]() если
если ![]()
4. Отметить, что от любой точки пространства можно отложить вектор, равный данному, и притом только один.
Дано: ![]() , М.
, М.
Доказать: существование ![]() - единственный вектор.
- единственный вектор.
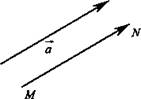
Доказательство: Проведем через начало и конец вектора ![]() и точку М плоскость и в этой плоскости построим
и точку М плоскость и в этой плоскости построим ![]() Из теоремы о параллельности прямых следует существование и единственность вектора
Из теоремы о параллельности прямых следует существование и единственность вектора ![]() где
где ![]()
IV. Закрепление изученного материала
№ 320 а. Дано: ABCD - тетраэдр. Точки М, N, К - середины АС, ВС, CD; соответственно, АВ = 3 см; ВС = 4 см; BD = 5 см.
Найти: ![]()
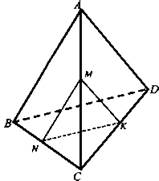
Решение: По условию задачи известно, что М, N, К - середины сторон АС, ВС, CD соответственно, поэтому МК - средняя линия ΔACD, NK - средняя линия ΔBCD. ![]()
![]()
![]() (Ответ: 3 см, 4 см, 5 см, 1,5 см, 2 см, 2,5 см.)
(Ответ: 3 см, 4 см, 5 см, 1,5 см, 2 см, 2,5 см.)
№ 322 (устно)
Вспомните свойства граней и диагоналей параллелепипеда.
По рисунку учебника учащиеся называют все пары:
а) сонаправленных векторов ![]()
б) противоположно направленных векторов ![]()
![]()
в) равных векторов ![]()
№ 326 (устно)
(Ответы: ![]() )
)
V. Самостоятельная работа (обучающая)
Работы учащихся, справившихся раньше других, можно оценить.
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, AD = 8 см, АВ = 9 см, АА1 = 12 см.
Найти: ![]()
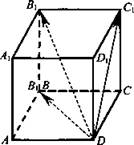
Решение: По свойству параллелепипеда ![]() По теореме Пифагора
По теореме Пифагора ![]()
![]()
![]() (Ответ: а) 12 см, 8 см, 9 см; б) 15 см, √145 см, 17 см.)
(Ответ: а) 12 см, 8 см, 9 см; б) 15 см, √145 см, 17 см.)
№ 323. Дано: DABC — тетраэдр, ребра которого равны. М, N, Р, Q - середины сторон АВ, AD, DC, ВС.
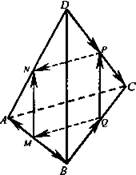
а) выписать пары равных векторов;
б) определить вид четырехугольника MNPQ.
Решение:
а) ![]()
б) Так как N, Р, М, Q - середины сторон соответственно АВ, AD, DC, ВС, то NP – средняя линия ΔADC, a MQ - ΔАВС; ![]()
![]() значит, NP = MQ; MN - средняя линия ΔADB, a PQ – средняя линия ΔDBC.
значит, NP = MQ; MN - средняя линия ΔADB, a PQ – средняя линия ΔDBC. ![]() значит, MN = PQ. Так как все ребра тетраэдра равны, то он правильный. Скрещивающиеся ребра в нем перпендикулярны. Тогда BD ⊥ AC. Имеем:
значит, MN = PQ. Так как все ребра тетраэдра равны, то он правильный. Скрещивающиеся ребра в нем перпендикулярны. Тогда BD ⊥ AC. Имеем:
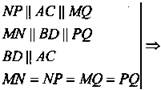 MNPQ – квадрат (Ответ: a)
MNPQ – квадрат (Ответ: a) ![]() б) квадрат.)
б) квадрат.)
VI. Подведение итогов
Домашнее задание
П. 34-35, № 320 (б) - I уровень; № 234 - II уровень.
Дополнительная задача
Дан правильный тетраэдр DABC. Точки М, N, К - середины ребер АВ, ВС и CD соответственно. Найдите: ![]() если
если ![]()
Решение домашнего задани.
№ 320. Дано: ABCD - тетраэдр, М ∈ АС, АМ = МС; N ∈ ВС, BN = NC; К ∈ CD, СК = KD. АВ = 3 см, ВС = 4 см, BD = 5 см.
Найти: ![]()
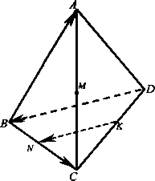
Решение: ![]()
![]() Так как N - середина ВС, то
Так как N - середина ВС, то ![]() KN - средняя линия ΔBCD.
KN - средняя линия ΔBCD. ![]() (Ответ: 4 см, 3 см, 5 см, 2 см, 2,5 см..
(Ответ: 4 см, 3 см, 5 см, 2 см, 2,5 см..
№ 324
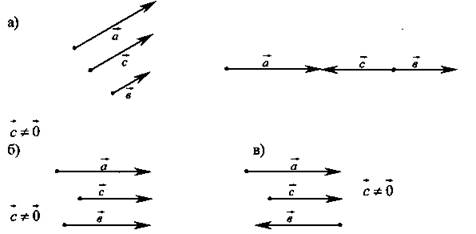
(Ответ: а) да; б) да; в) нет.)
Дополнительная задача
Дано: DABC - правильный тетраэдр. М, N, К - середины ребер АВ, ВС, CD соответственно. ![]()
Найти: ![]()
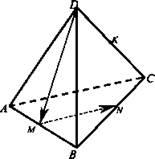
Решение: Так как тетраэдр правильный, то ΔADB - равносторонний. DM - высота, медиана и биссектриса. По теореме Пифагора, ![]() где
где ![]() По условию,
По условию, ![]()
![]()
2) MN - средняя линия ΔАВС: ![]() (Ответ: 1.)
(Ответ: 1.)