Поурочные разработки по геометрии 10 класс
Теорема о прямой, перпендикулярной к плоскости - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) повторить признак перпендикулярности прямой и плоскости;
2) доказать теорему существования и единственности прямой, перпендикулярной плоскости.
Ход урока
I. Организационный момент
Сообщить тему урока и сформулировать цели.
II. Повторение. Проверка домашнего задания
а) Сильный учащийся у доски повторяет доказательство признака перпендикулярности.
б) Проверяется решение дополнительной задачи.
в) Слабый учащийся по карточке на первой парте решает задачу;
В треугольнике ABC ∠C = 90°, АС = 12 см, ВС = 16 см, СМ - медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника ABC, СК = 24 см. Найти КМ. (26 см).
г) Фронтальный опрос учащихся по формулировкам из пунктов 15-17 и работа по готовым чертежам:
1. Сформулировать лемму о перпендикулярности двух параллельных прямых к третьей прямой.
2. Какая прямая называется перпендикулярной к плоскости?
3. Сформулировать теоремы, которые устанавливают связь между параллельностью прямых и их перпендикулярностью к плоскости.
4. Сформулировать признак перпендикулярности прямой и плоскости.
5. Можно ли утверждать, что прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости: двум сторонам треугольника (да); двум сторонам квадрата (нет); диагоналям параллелограмма (да) (рис. 1).

6. Дано: ABCD - куб (рис. 2).
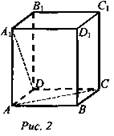
Заполните пропуски о взаимном расположении прямых и плоскостей.
![]()
III. Изучение нового материала
Формулируется и записывается в тетрадь теорема существования и единственности плоскости, проходящей через любую точку пространства перпендикулярно к данной прямой (это задача № 133 учебника). Доказательство разбирается учащимися самостоятельно по учебнику (стр. 40).
- Сформулируйте обратную теорему.
Записывается и доказывается теорема: через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна (используется рис. 50 учебника).
IV. Закрепление изученного материала
Задача № 122 (рис. 3)
Найти: АК, DA, BD.
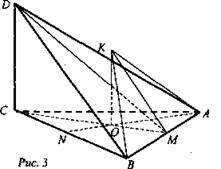
Решение:
1. BD = AD, так как ΔBCD = ΔACD (как прямоугольные, по двум катетам).
![]()
3. АК = ВС, так как ΔАОК = ΔВОК (как прямоугольные, по двум катетам).
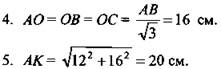
(Ответ: АК = ВК = 20 см; AD = BD = 32 см..
Задача № 125 (рис. 4).
Найти: P1Q1.
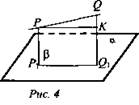
Решение:

1) Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; AD = 9 дм; DC = 8 дм; DВ1 = 17 дм (рис. 5).
Найти: SBB1D1D.
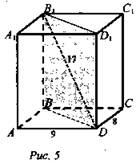
Решение: ΔADB: ∠BAD = 90°; AB = DC= 8 дм. По теореме Пифагора ![]()
![]() ΔB1BD: ∠B1BD = 90°. По теореме Пифагора
ΔB1BD: ∠B1BD = 90°. По теореме Пифагора ![]()
![]()
![]() (Ответ:
(Ответ: ![]() )
)
2) Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; AD1 = 8 м; DC1 = 10 м; DB = 12 м (рис. 6).
Найти: AD, DC, DD1.
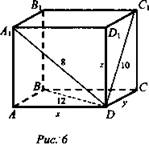
Решение: Обозначим AD = х (м); DD1 = z (м); DC = y(м). Из ΔAA1D: по теореме Пифагора ![]() Из ΔDCC1: по теореме Пифагора
Из ΔDCC1: по теореме Пифагора ![]() Из ΔABD: по теореме Пифагора
Из ΔABD: по теореме Пифагора ![]() получим систему:
получим систему:
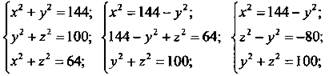
Сложим почленно 2 и 3 уравнения.
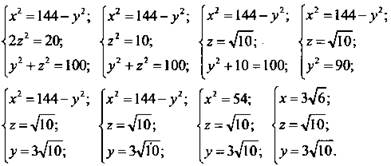
(Ответ: ![]() )
)
V. Подведение итогов
Смоделируйте в классной комнате описанную ниже ситуацию: Три луча ОМ, ОК, ОТ попарно перпендикулярны. Как расположен каждый из лучей по отношению к плоскости, определяемой двумя другими лучами? (Угол; перпендикулярно).
Домашнее задание
1) пункт 18.
2) № 123, 127.
Дополнительная задача
Точка А принадлежит окружности, АК - перпендикуляр к ее плоскости, АК = 1 см, АВ - диаметр, ВС - хорда окружности, составляющая с АВ угол 45°. Радиус окружности равен 2 см. Докажите, что треугольник КВС прямоугольный, и найдите КС. (3 см.)
Дано: окружность (О; R = 20 см); ВС - хорда, АВ - диаметр; ∠AВС = 45°, АК = 1 см; АК ⊥ (ABC) (рис. 7).
Доказать: ΔКВС - прямоугольный.
Найти: КС.
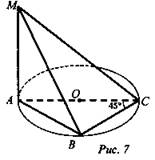
Решение:
1) ∠АСВ вписан в окружность, опирается на диаметр АВ ⇒ ∠AВС = 90° ⇒ ΔАСВ - прямоугольный и равнобедренный.
2) R = ОА = 2 см ⇒ АВ = 4 см. По теореме Пифагора АС = ВС = 2√2 см.
 Значит, ΔКСВ - прямоугольный (по теореме, обратной теореме Пифагора). (Ответ: 3 см.)
Значит, ΔКСВ - прямоугольный (по теореме, обратной теореме Пифагора). (Ответ: 3 см.)
Задача № 127
Дано: ![]() (рис. 8.)
(рис. 8.)
Доказать: CD ⊥ АС.
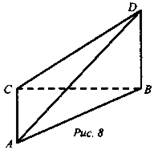
Доказательство:
1) ![]() ΔАВС - прямоугольный.
ΔАВС - прямоугольный.
2) ![]()
![]() Значит, AC ⊥ DC.
Значит, AC ⊥ DC.