Закрепление свойств параллелепипеда - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цель урока:

- подготовка к контрольной работе.

I уровень

Задача 1

Дано: ABCD - параллелограмм, АА1 и СС1. Прямые АА1 и СС1 не лежат в одной плоскости параллелограмма (рис. 1).

Доказать: (А1АВ) || (C1CD).

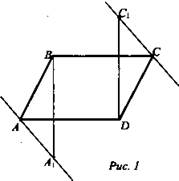
Решение: АВ || CD - противоположные стороны параллелограмма, АА1 || СС1 по условию. BA ∩ AA1 = A, DC ∩ СС1 = С. По признаку параллельности плоскостей (А1АВ) || (C1CD). Что и требовалось доказать.

Задача 2

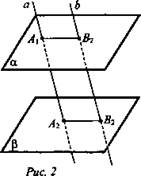
Дано: (рис. 2).

а) Доказать: А1В1 || А2В2.

б) Найти: ∠А2А1В1.

Решение:

а) Из определения параллельных прямых в пространстве следует, что прямые а и b лежат в одной плоскости, которая пересекает параллельные плоскости α и β по прямым А1В1 и А2В2. По 1° свойству параллельных плоскостей А1В1 || А2В2. Что и требовалось доказать.

б) Отрезки А1А2 || В1В2, так как α || β по условию. А1В1 || А2В2 по выше доказанному. Значит, А2В2В1А1 - параллелограмм по определению. По свойству параллелограмма (сумма углов, прилежащих к одной стороне, равна 180°) Так как по условию (Ответ: ∠A2A1B1 = 40°.)

Задача 3

Дано: ABCD - параллелограмм. Прямые АА1 и СС1 не лежат в плоскости параллелограмма АА1 || СС1 (рис. 3).

Доказать: (A1AD) || (С1СВ).

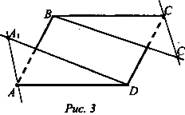
Решение: ВС || AD - противоположные стороны параллелограмма. СС1 || АА1 по условию; По признаку параллельности двух плоскостей (A1AD) || (С1СВ). Что и требовалось доказать.

Задача 4

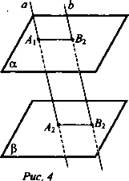
Дано: (рис. 4).

а) Доказать: А1В1 = А2В2.

б) Найти: ∠B1B2A2.

Решение:

а) Отрезки А1А2 и B1В2 параллельных прямых а и b параллельны, то есть А1А2 || B1B2. а || Р, α || β по условию. Следовательно, по свойству 2° параллельных плоскостей А1А2 = В1В2. Значит, противоположные стороны А1А2 и В1В2 четырехугольника А2В2В1А1 равны и параллельны и А2В2В1А1 - параллелограмм. В параллелограмме противолежащие стороны равны, поэтому А1В1 = A2В2, что и требовалось доказать.

б) В параллелограмме противоположные углы равны, ∠B1A1A2 = ∠B1B2A2, так как ∠B1A1A2 = 50°, то ∠B1B2A2 = 50°. (Ответ: ∠B1B2A2 = 50°.)

II уровень

Задача 5

Дано: ABCD и A1B1CD параллелограммы не лежат в одной плоскости (рис. 5).

Доказать: (ADA1) || (ВСВ1).

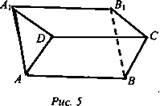
Решение:

противоположные стороны параллелограммов AD ∩ DA = D; В1С ∩ СВ = С. По признаку параллельности двух плоскостей (ADA1) || (ВСВ1).

Задача 6

Дано: (рис. 6).

Доказать: a) АВ || CD; б) ∠ADC четырехугольника ABCD равен 65°.

Найти остальные углы.

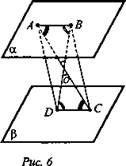
Решение: Прямые АС и BD пересекаются и задают плоскость ABCD. По свойству параллельных плоскостей (п. 11, 1°) АВ || CD, ΔAОВ = ΔDOC по второму признаку как внутренние накрест лежащие при параллельных АВ и DC и секущей BD и АС для второй пары. АВ = DC по условию.

Из равенства треугольников следует, что OB = OD, АО = СО, то есть диагонали четырехугольника делятся точкой пересечения пополам. Значит, ABCD - параллелограмм. У параллелограмма противоположные углы равны. Если ∠ADC = 65 °, то ∠ABC = 65 °, ∠DAB = 180° - ∠ADC = 180° - 65° = 115°. ∠BCD = ∠DAB = 115°. (Ответ: 65°, 115°, 115°.)

Задача 7

Дано: ABCD и ABC1D1 - параллелограммы не лежат в одной плоскости (рис. 7).

Доказать: (СВС1) || (DAD1).

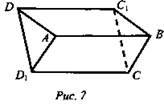
Решение: по определению параллелограмма Имеем две пересекающиеся прямые одной плоскости, соответственно параллельны двум пересекающимся прямым другой плоскости. Следовательно, по признаку параллельности двух плоскостей (СВС1) || (DAD1). Что и требовалось доказать.

Задача 8

Дето: D = О, АВ = CD, ∠BAD = 130° (рис. 8).

а) Доказать: AD || ВС.

б) Найти: ∠ABC, ∠ADC, ∠BCD.

Решение:

а) Две пересекающиеся прямые единственным образом задают плоскость. Отрезки АС и BD пересекаются и задают плоскость ABCD, которая пересекает параллельные плоскости аир по прямым АВ и DC. По свойству 1° параллельных плоскостей АВ || DC. АВ = DC по условию.

Поэтому четырехугольник ABCD - параллелограмм. Значит, AD || ВС. Что и требовалось доказать.

б) В параллелограмме сумма углов, прилежащих к одной стороне равна 180°. В параллелограмме противоположные углы равны. ∠BAD = ∠BCD, ∠ABC = ∠ADC. Так как ∠BAD = 130°, то ∠BCD = 130°, ∠ADC = 50°, то и ∠ABC = 50°. (Ответ: ∠BCD = 130°, ∠ADC = 50°, ∠ABC = 50°.)

III уровень

Задача 9

Дано: (рис. 9).

При каком взаимном расположении прямых а и b α || β?

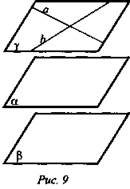
Решение: α || β, если прямые а и b пересекаются.

Две пересекающиеся прямые единственным образом задают плоскость. Прямые а и b пересекаются и задают плоскость γ. Пересекающиеся прямые а и b плоскости γ параллельны плоскости α. Значит, α || γ (задача 51). Рассуждая аналогично, имеем β || γ, α || γ, α || у. Следовательно, α || β (задача 60).

Задача 10

Дано: α || β. Отрезки АС и BD пересекаются в точке О, (рис. 10).

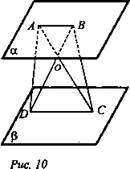
а) При каком дополнительном условии пересечения отрезков ABCD - прямоугольник?

б) Доказать: ABCD - равнобокая трапеция.

а) Две пересекающиеся прямые единственным образом задают плоскость.

Отрезки АС и BD пересекаются и задают плоскость ABCD. По 1° свойству параллельных плоскостей АВ || CD. По условию АС = BD. При дополнительном условии, что пересекающиеся отрезки делятся точкой пересечения пополам, ABCD будет являться прямоугольником.

б) Из выше доказанного АВ || CD. Значит, ABCD - трапеция по определению. AC || BD - ее диагонали. Если диагонали трапеции равны, то она равнобедренная. АС = BD по условию.

Значит, ABCD - равнобокая трапеция.

Задача 11

Дано: (рис. 11).

При каком взаимном расположении прямых а и b α || β?

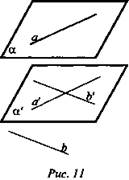
Решение: и а и b скрещивающиеся прямые; если прямые а и b скрещивающиеся или параллельные.

Задача 12

Дано: (рис. 12).

а) При каком дополнительном условии пересечения отрезков ABCD - квадрат?

б) Доказать, что ABCD трапеция, в которой высота равна средней линии.

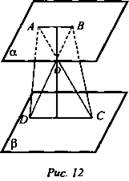
Решение:

а) По свойству 1° параллельных АВ || DC. При условии, что отрезки точкой пересечения делятся пополам, ABCD будет являться квадратом.

б) ΔBDC = ΔADC (по двум сторонам и угу между ними. DC - общая, AD = BC, ∠ADC = ∠BCD как углы при основании равнобедренной трапеции).

Из равенства треугольников следует, что ∠BDC = ∠ACD. Тогда DO = ОС. ΔDOC - прямоугольный и равнобедренный. ОМ - высота,, биссектриса, медиана. ΔОМС - прямоугольный равнобедренный. ОМ = МС или ОМ = 1/2DC.

Аналогично где MN - высота, 1/2(DC + ВА) - средняя линия трапеции.

Примечание: Задачи решаются учащимися самостоятельно. Уровень выбирают ученики. Анализ решений делает учитель.