Поурочные разработки по геометрии 10 класс
Параллелепипед - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие параллелепипеда;
2) рассмотреть его свойства 1° и 2°;
3) решить задачи на применение свойств параллелепипеда.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний
1) Двое учеников на доске записывают решение домашнего задания: № 67 - первый, № 70 - второй.
Задача 67
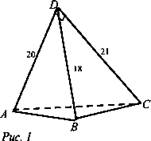
Дано: DABC - тетраэдр, ∠ADB = 54°, ∠BDC = 72°, ∠CDA = 90°, DA = 20 см, ВD = 18 см, DC = 21 см (рис. 1).
Найдите: а) АВ; ВС; б) SADB, SABC, SADC.
Решение:
а) 1. Из ΔADB (∠ADB = 54°) по теореме косинусов; АВ2 = AD2 + DB2 - 2 · AD · BD · cos 54° ≈ 298; АВ ≈ 17 см.
2. Из ΔBCD (∠BCD = 72°); ВC2 = BD2 + CD2 - 2 · BD · CD · cos 72° ≈ 529; ВС ≈ 23 см.
3. Из ΔCDA (∠ADC = 90°) по теореме Пифагора; АС2 = AD2 + DC2 = 202 + 212 = 841; AС = 29 см; SΔ = 1/2а · b · sin α.
б) ![]()
![]() (Ответ: a) ≈ 17 см, ≈ 23 см, 29 см; б) ≈ 146 см2, ≈ 180 см2, 210 см2.)
(Ответ: a) ≈ 17 см, ≈ 23 см, 29 см; б) ≈ 146 см2, ≈ 180 см2, 210 см2.)
Задача 70
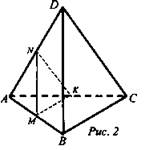
Дано: ABCD - тетраэдр, AM = MB, AN = ND, AK = KC (рис. 2).
Доказать: (MNK) || (BCD).
Решение:
1. MK || ВС (по свойству средней линии Δ).
2. MN || BD (по свойству средней линии Δ).
![]() (по признаку параллельности двух плоскостей).
(по признаку параллельности двух плоскостей).
2) Ученик решает задачу № 71 (а), объясняя вслух.
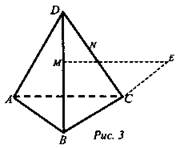
Дано: DABC - тетраэдр, М ∈ DB, N ∈ DC (рис. 3).
Построить: точку Е.
Условие: MN ∩ (ABC) = Е.
Решение:
1. MN ∩ (DCB);
2. (DCB) ∩ (АВС) = ВС;
3. Продолжим ВС и MN, ВС ∩ MN = E1; Е - искомая точка.
3) Остальные устно решают задачи по готовым чертежам.
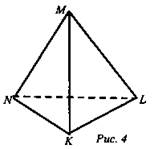
1. Укажите все грани, ребра, вершины, противоположные ребра, скрещивающиеся ребра тетраэдра (рис. 4).
4. Что называется параллелограммом? Свойства параллелограмма? Признаки параллелограмма?
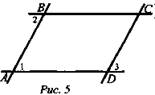
Дано: ∠1 = ∠2 = ∠3 (рис. 5).
Доказать, что четырехугольник ABCD - параллелограмм.
Проверяется домашнее задание.
III. Изучение нового материала
1) Понятие параллелепипеда.
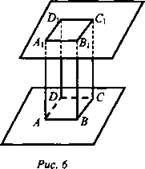
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, CC1 и DD1 параллельны. Четырехугольники АВВ1А1, ВСС1В1, CDD1C1, DAA1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны (например, в ABB1A1 стороны АА1 и ВВ1 параллельны по условию, а АВ и А1В1 - по свойству линий пересечения двух параллельных плоскостей третьей).
Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1, лежащих в параллельных плоскостях и четырех параллелограммов, называется параллелепипедом и обозначается так: ABCDA1B1C1D1 (рис. 6).
2) Элементы параллелепипеда.
Параллелограммы, из которых составлен параллелепипед, называются гранями, их стороны -ребрами, а вершины - вершинами параллелепипеда.
Сколько граней имеет параллелепипед? ребер? вершин?
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер - противоположными.
Две вершины, не принадлежащие одной грани, называются противоположными.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Сколько диагоналей имеет параллелепипед?
Выделяют две противоположные грани и называют их основаниями, а остальные грани - боковыми.
Ребра параллелепипеда, не принадлежащие основаниям, называются боковыми ребрами.
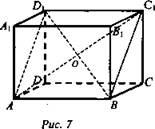
Изображение (рис. 7).
3) Свойства параллелепипеда.
1° Противоположные грани параллелепипеда параллельны и равны.
Дано: ABCDA1B1C1D1- параллелепипед (рис. 8).
Доказать: a)ABB1A1 || DCC1D1; б) АВВ1А1 = DCC1D1.
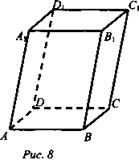
Доказательство:
а) Так как ABCD и ADD1А1 - параллелограммы, то АВ || DC, АА1 || DD1. Тогда АВ ∩ AA1 одной плоскости параллельны двум пересекающимся прямым DC ∩ DD1 другой плоскости. Значит, АВВ1А1 || DCC1D1 (по признаку параллельности плоскости).
б) Так как все грани параллелепипеда - параллелограммы, то АВ = DC, АА1 = DD1. По той же причине стороны (А1АВВ1) и (D1DCC1) соответственно сонаправлены, значит, ∠А1АВ = ∠D1DC. Таким образом АВВ1А1 = DCC1D1.
2° Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Дано: ABCDA1B1C1D1 - параллелепипед (рис. 9).
Доказать: AC1 ∩ BD1 = О, АО = ОС1, OD1 = BO.
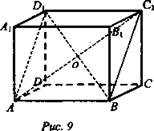
Доказательство:
Рассмотрим AD1C1B, ![]()
![]() значит, AB = D1C1 ⇒ AD1C1B - параллелограмм, а диагонали
значит, AB = D1C1 ⇒ AD1C1B - параллелограмм, а диагонали ![]()
Аналогично рассматриваются следующие случаи для A1D1CB и A1B1CD. Вывод (устно).
IV. Закрепление изученного материала
1) (Устно) Укажите: а) вершины, не лежащие в плоскости ABC; б) грани, пересекающиеся в точке В; в) ребра, параллельные ребру CD; параллельные плоскости BCF.
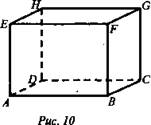
2) (Устно) В параллелепипеде ABCDEFGH диагонали ВН и СЕ пересекаются в точке О, ВО = 3 см, СО = 5 см (рис. 10).
Найдите ВН и СЕ.
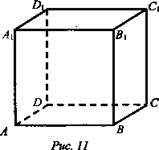
3) № 77. Дано: ABCDA1B1C1D1 - параллелепипед; ![]()
![]() (рис. 11).
(рис. 11).
Найти: АВ, ВС, ВВ1.
Решение: х - коэффициент пропорциональности. Пусть АВ = 4х, ВС = 5х, ВВ1 = 6х. По условию ![]()
![]() Значит, АВ = 8 см, ВС = 10 см, ВВ1 = 12 см. (Ответ: 8 см, 10 см, 12 см.)
Значит, АВ = 8 см, ВС = 10 см, ВВ1 = 12 см. (Ответ: 8 см, 10 см, 12 см.)
4) № 112. Дано: ABCDA1B1C1D1 - параллелепипед (рис. 12).
Доказать: ![]()

Решение:
1. Для параллелограмма ABCD: АС2 + BD2 = 2(АВ2 + ВС2).
2. Из параллелограмма АА1С1С: АС12 + А1С2 = 2(AA12 + АС2).
3. Из параллелограмма BDD1B1: BD12 + B1D2 = 2(BD2 + ВВ12).

IV. Подведение итогов
Домашнее задание
П. 13, вопросы 14, 15, № 76, 78.
Дополнительная задача 103
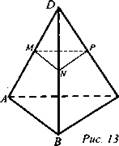
Дано: DABC тетраэдр, М ∈ DA, N ∈ DB и P ∈ DC, ![]() (рис. 13).
(рис. 13).
Доказать: (MNP) || (ABC).
Найти: SΔMNP.
Решение:
а) 1. Рассмотрим ΔADB и ΔMDN. ∠D - общий; ![]()
![]() (по условию),
(по условию), ![]()
![]() или
или ![]() ΔADB ~ ΔMDN (no углу и пропорциональным сторонам).
ΔADB ~ ΔMDN (no углу и пропорциональным сторонам).
2. Из подобия Δ следует: ∠1 = ∠2, ∠3 = ∠4. ⇒ MN || АВ.
3. ΔBDC ~ ΔNDP - аналогично, используя ![]()
4. MN || AB и NP || BC ⇒ (MNP) || (ABC) (по признаку параллельности двух плоскостей).
б) 1. ΔАВС ~ ΔMNP (по двум углам); ![]()
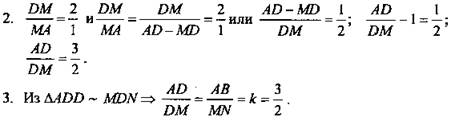
![]() (Ответ:
(Ответ: ![]() )
)