Тетраэдр - ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цели урока:

1) повторить понятие многоугольника в планиметрии;

2) ввести понятие тетраэдра;

3) рассмотреть задачи, связанные с тетраэдром.

Ход урока

I. Организационный момент

Сообщить тему урока, сформулировать цели урока.

II. Проверка домашнего задания

1) Один ученик записывает на доске решение домашней задачи № 63 а.

Дано: (рис. 1).

Найти: АА2, АВ2.

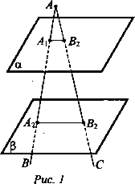
Решение:

1. A1B1 || А2В2 (по свойству 1° параллельных плоскостей).

2.

3. Так как A1A2 = 2 A1A и А1А2 = 12 см, то A1A = 12 : 2 = 6 см.

4. АА2 = 12 + 6 = 18 см.

5. (Ответ: АА2 = 18 см, АВ2 = 15 см.)

2) Двое решают по карточкам индивидуального опроса.

I. Отрезки АВ, АС и AD не лежат в одной плоскости. Точки К, М и N - соответственно их середины.

а) Докажите, что плоскости BCD и KMN параллельны.

б) Найдите площадь ΔВСD, если SKMN = 36 м2. (Ответ: SBCD = 144 м2.)

II. Три прямые, проходящие через точку М и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А1, В и С, а вторую - в точках А1, В1 и С1.

а) Докажите, что ABC ~ ΔA1B1C1.

б) Найти если МС = CC1. (Ответ: 1/2.)

3) Остальные отвечают на вопросы (устно).

1) Каково взаимное расположение двух плоскостей, если третья плоскость пересекает их по прямым: а) имеющим общую точку; б) не имеющим общих точек?

2) Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть ее боковыми сторонами?

3) Каким может быть взаимное расположение двух прямых, если эти прямые пересекают две параллельные плоскости, и их отрезки, заключенные между плоскостями, не равны?

4) Две плоскости пересечены двумя параллельными прямыми. Выясните взаимное расположение этих плоскостей, если отрезки данных прямых, заключенные между этими плоскостями, не равны.

5) Прямая а пересекает параллельные плоскости α и β в точках А и В. Прямая b, параллельная прямой а, пересекает плоскости в точках D и С. Найдите периметр четырехугольника ABCD, если АВ = 3 см, ВС = 4 см.

6) Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.

III. Изучение нового материала

Использовать модели нескольких тетраэдров, а также гибкую модель из картона и ниток (рис. 2).

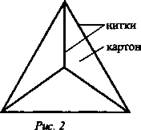
1) Одна из глав нашего курса будет посвящена многогранникам - поверхностям геометрических тел, составленных из многоугольников. Познакомимся с одним из них сегодня на уроке - тетраэдром. Это даст нам возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей на примере геометрических тел.

Вспомним, прежде всего, что мы понимали под многоугольником в планиметрии. (Ответы).

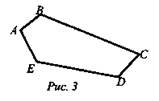
Учитель обобщает ответы учащихся: многоугольник мы рассматривали либо как замкнутую линию без самопересечений, составленную из отрезков (рис. 3), либо как часть плоскости, ограниченную этой линией, включая ее саму (рис. 4).

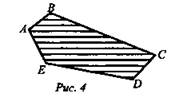
При рассмотрении поверхностей и тел в пространстве будем пользоваться вторым толкованием многоугольника. При. таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность.

2) Определение тетраэдра. Построим ΔАВС; точка D, не лежащая в плоскости этого треугольника. Соединив точку D отрезками с вершинами ΔABC, получим ΔDAB, ΔDBC, ΔDCA, получим тетраэдр.

Итак, поверхность, составленная из четырех треугольников ΔABC, ΔDAB, ΔDBC и ΔDCA, называется тетраэдром и обозначается: DABC.

Тетраэдр, то есть четырехгранник («тетра» - четыре, «эдр» - грань). (Показ моделей тетраэдров.)

3) Треугольники, из которых состоит тетраэдр, называются гранями, их стороны - ребрами, а вершины - вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть ребер и четыре вершины.

Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. На рис. 34 учебника AD и ВС, BD и АС, CD и АВ.

Иногда выделяют одну из граней тетраэдра и называют ее основанием, а три другие - боковыми гранями.

4) Изображение тетраэдра на плоскости (рис. 5).

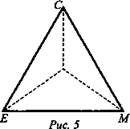
IV. Закрепление изученного материала

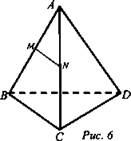
1) № 68 (устно) по готовому чертежу (рис. 6).

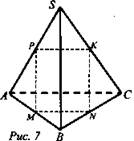
2) № 69. Дано: SABC - тетраэдр, МА = MB, BN = NC, (рис. 7).

Доказать: PM|| KN.

1. (по свойству 1°).

2. (по свойству 1°).

3. BS || KN, BS || PM, KN || РМ (по теореме о параллельности трех прямых).

3) № 716. Дано: DABC - тетраэдр, M ∈ DB, N ∈ DC, К ∈ ВС (рис. 8).

Построить: точку М1.

Условие: M1 = KN ∩ (FBD).

Решение:

1. NK ⊂ (DBC), DB ⊂ (DBC).

2. NK не может быть параллельна прямой DB. Так как NK || (ADB) (по признаку) - это противоречит условию ⇒ NK ∩ DB.

3. DB ⊂ (ADB), то NK ⊂ (ADB) = М1.

4) № 73. Дано: DABC — тетраэдр, М ∈ АВ, N ∈ BC, Р ∈ CD, K ∈ AD; МА = MB, NB = NC, PC = PD, AC = 10 см, BD = 12 см, AK = KD (рис. 9).

Доказать: К ∈ (MNP).

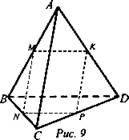
Найти: PMNPK.

Решение:

1. (MNP) ∩ (ABC) = MN, MN - средняя линия ΔABC ⇒ MN || AC.

2. MN || (ACD) (по признаку параллельности прямой и плоскости), MN проходит через (MNP), (MNP) || (ACD). Значит, линия пересечения (MNP) и (ACD) параллельна MN.

3. Пусть эта линия пересекается с ребром AD в точке К. Так как РК || MN и MN || АС, то РК || АС, а так как Р - середина AD, то РК - средняя линия ΔACD, то есть К - середина AD.

4. (Ответ: 22 см.)

V. Подведение итогов

Домашнее задание

П. 12, I уровень: № 67 (a), 70; II уровень: № 67, 71 (a).