Поурочные разработки по геометрии 10 класс
Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми» - ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) закрепление теоретического материала;
2) совершенствование навыков решения задач по данной теме.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Теоретический опрос:
а) один ученик доказывает признак скрещивающихся прямых;
б) второй ученик доказывает теорему о скрещивающихся прямых;
в) третий ученик доказывает теорему об углах с сонаправленными сторонами.
2. Проверка домашнего задания (на переносной доске): а) один ученик решает № 40 из домашнего задания, б) второй ученик решает № 42 из домашнего задания.
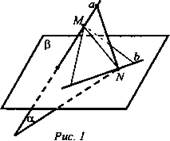
№ 40. Дано: а и b - скрещивающиеся прямые; γ - плоскость, а ∉ γ, b ∈ γ. Точка M ∈ а, точка N ∈ b. Через а и N проведена плоскость α. Через b и М проведена плоскость β (рис. 1).
Найти: а) лежит ли прямая b в плоскости α? б) пересекаются ли плоскости α и β?
Решение:
а) Если бы b ∈ α, тогда в плоскости α было бы две возможности:
1) b || а - но это противоречит условию;
2) b ∩ а - но это противоречит условию; b ∩ α в точке N, N ∉ а.
Вывод: b ∉ α.
б) ![]() прямая MN - общая для плоскостей α и β.
прямая MN - общая для плоскостей α и β.
Вывод: α ∩ β по прямой MN.
(Ответ: b ∉ α, MN - прямая, по которой α ∩ β).
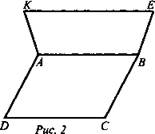
№ 42. Дано: ABCD - параллелограмм; АВЕК - трапеция: ЕК - основание; ЕК ∉ (ABCD) (рис. 2).
а) Выясните взаимное расположение прямых CD и ЕК.
б) Найти: Р(ABEK), если АВ = 22,5 см; ЕК = 27,5 см.
Решение:
1. CD || АВ - как противолежащие стороны параллелограмма АВ || ЕК - по определению трапеции. Значит, CD || ЕК.
2. Так как в трапецию можно вписать окружность, то АВ + КЕ = BE + АК. Тогда Р(ABEK) = (22,5 + 27,5) · 2 = 50 · 2 = 100 (см). (Ответ: a) CD || ЕК; б) Р(ABEK) = 100 см.)
Остальные учащиеся отвечают на вопросы математического диктанта.
Вариант I
1. Какие две прямые в пространстве называются параллельными?
2. Сформулируйте признак параллельности прямой и плоскости.
3. Какие возможны случаи взаимного расположения прямой и плоскости?
4. Дан куб ABCDA1В1C1D1. Запишите четыре пары параллельных прямых.
5. Верно ли утверждение: если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость.
Вариант II
1. Какие прямая и плоскость называются параллельными?
2. Сформулируйте теорему о параллельных прямых.
3. Сформулируйте признак параллельности прямой и плоскости.
4. Дан куб ABCDA1B1C1D1. Запишите четыре пары пересекающихся прямых.
5. Верно ли утверждение: если одна из двух прямых параллельна плоскости, а вторая пересекает эту плоскость, то прямые параллельны.
Далее проверяется решение домашнего задания, написанного на доске, а математический диктант собирается учителем и проверяется.
III. Решение задач
№ 38. Чертеж на доске, решение обсуждается устно.
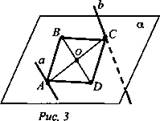
Дано: ABCD - ромб; а || BD; А ∈ а; b ∈ (ABCD); с ∈ b (рис. 3).
Доказать: a) a ∩ CD; б) а и b - скрещивающиеся прямые.
Доказательство:
А) 1. Прямая а проходит через точку А ∈ α, и а || BD (по условию), BD ∈ α, значит, а ∈ α.
2. ![]()
Б) ![]() в точке D ⇒ (по теореме п. 7) а и b - скрещивающиеся прямые, что и требовалось доказать.
в точке D ⇒ (по теореме п. 7) а и b - скрещивающиеся прямые, что и требовалось доказать.
Определение:
Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости.
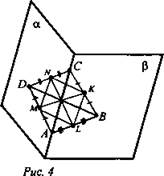
№ 43. Дано: ABCD - пространственный четырехугольник; L - середина АВ; К - средина ВС; N - средина DC; М - средина DA (рис. 4).
Доказать: LKNM - параллелограмм.
Решение:
1) LK - средняя линия ΔАВС, ![]()
![]()
2) MN - средняя линия ΔADC, ![]()
![]()
3) ML - средняя линия ΔADB, ![]()
4) NK - средняя линия ΔCBD, ![]()
5) ![]()
6) Построим плоскость MNKL, которая по определению параллелограмма будет являться параллелограммом.
Вывод: MNKL - параллелограмм.
IV. Подведение итогов
Домашнее задание
П. 4—9, вопросы: № 1-8, 1 глава; № 45; 47; 90. № 90 - 1 уровень; № 45 – II уровень; № 47 - III уровень.