Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Образцы вариантов экзаменационных билетов
Московский государственный университет им. M. В. Ломоносова (МГУ) (экономический факультет)
1. Решите уравнение
3|x| = 5x² + 3x.
2. Решите систему неравенств
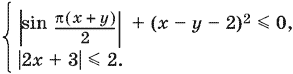
3. В треугольнике АВС со стороной AB = √5 из вершины В к стороне AC проведены медиана ВМ = 2√2 и высота ВН = 2. Найдите сторону ВС, если известно, что ∠АВС + ∠ACВ < 90°.
4. Банк планирует вложить на один год 40% имеющихся y него средств клиентов в проект X, а остальные 60% — в проект Y. В зависимости от обстоятельств проект X может принести прибыль в размере от 19 до 24% годовых, а проект Y — от 29 до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определите наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты X и Y.
5. Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4, и на промежутке 0 ≤ x ≤ 2 ее значения вычисляются по правилу f(x) = 1 − |x − 1|. Решите уравнение
2 f(x) f(x − 8) + 5 f(x + 12) + 2 = 0.
6. Найдите все значения параметра а, при которых периметр фигуры, заданной на координатной плоскости условием
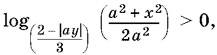
будет наименьшим.