Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Образцы вариантов экзаменационных билетов
Московский государственный технический университет им. Н. Э. Баумана (МГТУ)
1. Из пункта А в пункт В одновременно вышли два пешехода. Когда первый прошел половину пути, второму осталось пройти 24 км, а когда второй прошел половину пути, первому осталось пройти 15 км. Найдите расстояние от пункта А до пункта В.
2. Найдите все корни уравнения
cos 2x + cos 6x = cos 4x,
принадлежащие промежутку [π/2; π].
3. Решите уравнение
![]()
4. Решите неравенство 2x + 1 + 3 < 21 − x.
5. Какая наибольшая площадь может быть y прямоугольного треугольника, одна вершина которого совпадает с точкой M(5; 0), другая лежит на графике функции y = x³(5 − x), 0 ≤ x ≤ 5, а вершина прямого угла — на оси Ox?
6. Найдите все значения p, при которых система уравнений
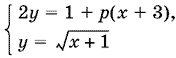
имеет единственное решение.
7. Основанием пирамиды ТАВС служит треугольник АВС с углом А, равным 60°. Боковое ребро ТА совпадает с высотой пирамиды и равно h; ребро ТС перпендикулярно стороне основания ВС, а угол между ребром ТВ и биссектрисой основания АD равен 60°. Какую наименьшую площадь может иметь сечение пирамиды плоскостью, проходящей через биссектрису АD и пересекающую ребро ТВ?