Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003

Решения
Задачи на составление уравнений

18.1. Пусть x, y, z, u — производительности первой, второй, третьей и четвертой труб соответственно. Примем объем бассейна за единицу. Тогда получим систему уравнений

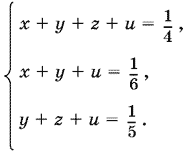
Вычитая из первого уравнения поочередно второе и третье, найдем соответственно

z = ¹/₁₂, x = ¹/₂₀.

Следовательно, общая производительность первой и третьей труб равна z + x = ²/₁₅.

Ответ. 7,5 ч.

18.2. Пусть плечи весов равны l₁ и l₂ соответственно. Тогда в первый раз продавец отпустил

кг товара, а во второй раз он отпустил

кг. Таким образом, он отпустил покупателю товар массой

В силу неравенства между средним арифметическим и средним геометрическим

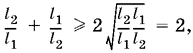
где равенство достигается лишь при l₁ = l₂. Таким образом, продавец отпустил больше товара, чем следовало.

18.3. Если все 500 марок расклеить по 20 на один лист, то двух альбомов не хватит для всех марок. Поэтому 2x < 25, т. е. x ≤ 12 (x − количество листов в альбоме и, следовательно, целое). Если же 500 марок расклеить по 23 на один лист, то в двух альбомах окажется по крайней мере один свободный лист. Это значит, что 2x − 1 ≥ ⁵⁰⁰/₂₃, откуда 2x ≥ 22, x ≥ 11. Итак, либо x = 11, либо x = 12.

Если в альбоме 11 листов, то y школьника было 500 − 21 · 11 = 269 марок, которые нельзя разместить на 10 листах по 23 штуки на каждом. Второе число удовлетворяет условию задачи.

Ответ. 12 листов.

18.4. Поскольку понтоны находились в пути одинаковое время и в одинаковых условиях, то каждый из них проплыл одно и то же расстояние без буксира (см. второе указание на с. 203). Обозначим это расстояние через x. Каждый понтон находился в пути

Буксир в свою очередь, помимо пути в l км вниз по течению, дважды преодолел расстояние l − 2x км: один раз вниз по течению, другой раз вверх по течению. На весь путь y него ушло

Приравниваем выражения (1) и (2) (буксир был в пути столько же времени, сколько каждый понтон) и решим уравнение.

Получим

Следовательно, второй понтон должен транспортироваться на расстояние в

а на всю перевозку уйдет

Ответ.

18.5. Пусть некто родился в

году, где x − число десятков, а y — число единиц. В 1901 году ему было 1901 −

лет.

Если y > 1, то, произведя вычитание, получим число

, где 9 − x и 11 − y — цифры, образующие это число.

По условию сумма цифр числа

равна сумме цифр числа

1 + 8 + x + y = (9 − x) + (11 − y), т. е. x + y = 5,5,

что невозможно, так как x и y — целые.

Если y ≤ 1 (это значит, что либо y = 0, либо y = 1), после вычитания получим число

, где 10 − x и 1 − y цифры, образующие это число. Когда x ≠ 0, это число состоит из двух цифр, а когда x = 0 — из трех, причем первые две цифры 1 и 0. Пусть x ≠ 0. Запишем сумму цифр для этого числа:

1 + 8 + x + y = (10 − x) + (1 − y), т. е. x + y = 1.

Так как x ≠ 0, то y = 0, а x = 1. Это означает, что некто родился в 1810 году.

Пусть теперь x = 0. Тогда получим уравнение

1 + 8 + y = 1 + (1 − y),

откуда y = −3,5, что невозможно.

Ответ. В 1810 году.

18.6. Пусть одна часть имеет массу x карат, тогда другая — p − x карат. Цена этих частей равна lх² и l(p − x)² соответственно, где l — коэффициент пропорциональности. Так как цена целого бриллианта была равна lр², то получим уравнение

lр² = k[lх² + l(p − x)²], которое после упрощений примет вид

Проведем исследование.

По смыслу задачи k > 1, p > 0. Следовательно, подкоренное выражение будет неотрицательным, если k ≤ 2, т. е. 1 < k ≤ 2.

Так как

(мы знаем, что k > 1), то оба значения x неотрицательны. Легко проверить, что p − x₁ = x₂.

Ответ.

18.7. Примем расстояние, которое туристам нужно пройти на моторной лодке, за единицу. Через x кг/ч обозначим расход горючего в течение часа работы двигателя в режиме, обеспечивающем собственную скорость лодки v₁, а через y кг/ч — расход горючего при работе двигателя во втором режиме (v₂). Весь путь лодка пройдет за

ч при работе двигателя в первом и во втором режимах соответственно. Так как расход горючего будет одинаковым, то

Если скорость течения реки будет равна ku, то из условия получим второе уравнение

Найдя из первого уравнения x, подставим во второе. Получим

откуда

Так как k > 1, то y > 0 только при v₂ > v₁ и ku < v₁. Общий расход горючего равен

Ответ.

18.8. Обозначим через x, y, z, s и t количество десятков порций стоимостью по 7, 9, 11, 13 и 15 p. за порцию соответственно.

Условия задачи можно переписать в виде системы

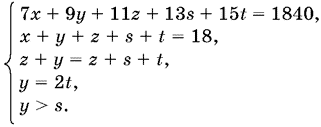
Вычитая из первого уравнения второе, умноженное на 7, получим

y + 2z + 3s + 4t = 29

или (так как y = 2t)

2z + 3s + 6t = 29.

В результате сравнения второго и третьего уравнений найдем

z + s + t = 9.

Умножим это уравнение на два и вычтем из предыдущего уравнения:

s + 4t = 11.

Поскольку s и t — натуральные, t может принимать лишь два значения: t = 1 и t = 2, иначе уравнение s + 4t = 11 не выполняется. Если t = 1, то s = 7, а y = 2. Это противоречит требованию y > s. Следовательно, t = 2, s = 3, y = 4. Нетрудно найти, что x = 5, z = 4.

Ответ. 50 порций мороженого по 7 p., 40 порций по 9 p., 40 порций по 11 p., 30 порций по 13 p., 20 порций по 15 p.

18.9. Обозначим время, за которое плоты прошли путь по озеру, через x. Так как весь путь они прошли за 11,5 суток, т. е. за 276 ч, то путь AC (буквой С обозначено устье реки) — за 276 − x ч, а скорость течения реки равна ^AC/_{276 − x}.

Выразим скорость течения реки с помощью остальных условий задачи. Если пароход проходит путь от А до В за 40 ч, а путь от С до В за x ч (идет в два раза быстрее, чем с плотами), то скорость парохода вниз по течению реки равна

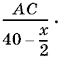
Аналогично его скорость вверх по течению равна

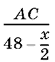
. Если вычесть из первой скорости вторую, то получим удвоенную скорость течения реки. Мы пришли к уравнению

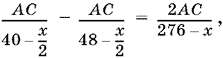
решая которое найдем: x₁ = 24, x₂ = 136. Второй корень посторонний, так как 40 − ^x/₂ и 48 − ^x/₂ становятся отрицательными, что не имеет физического смысла.

Ответ. 24 ч.

18.10. Пусть v₁, v₂ и v₃— скорости пловцов, а x − расстояние AC (рис. P.18.10).

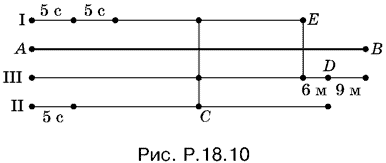
Приравниваем времена, за которые пловцы проплыли путь AC:

Из условия встречи в точке D третьего и второго пловцов получим

а из условия встречи в точке E третьего и первого:

Так как в уравнение (4) входят v₂ и v₃, а в уравнение (5) v₁ и v₃, то уравнения (3) перепишем в виде

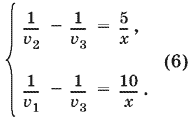
Преобразуем теперь уравнения (4) и (5):

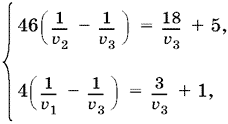
и воспользуемся заменой (6). Получим систему

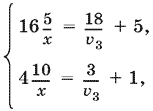
из которой проще исключить v₃. Найдем x = 10. Следовательно, v₃ = 1.

Ответ. 1 м/с.

18.11. Обозначим через x часть сосуда, занимаемую раствором кислоты, а объем всего сосуда примем за единицу. После того как сосуд долили q%−м раствором, количество концентрированной кислоты стало

^px/₁₀₀ + ^{q(1 − x)}/₁₀₀,

а новая концентрация

p₁ = px + q(1 − x) = (p − q)x + q.

Если вместо p подставить р₁, то получим р₂, аналогично можно получить р₃ и т. д. Приходим к рекуррентному соотношению

р_k = x(р_{k − 1} − q) + q.

Вычислим р₂:

р₂ = x(р₁ − q) + q = х²(p − q) + q.

По индукции легко доказать, что

р_k = x^k(p − q) + q.

Так как p_k = r, то получим уравнение

r = x^k(p − q) + q,

откуда

Ответ.

где либо r > q, p > q, либо r < q, p < q.

18.12. Пусть x и y — скорости автомобиля и мотоцикла соответственно, а z — длина пути AB. Тогда первая встреча произойдет через ^z/_{x + y} ч после начала движения на расстоянии ^zy/_{x + y} от пункта В. Те же рассуждения, примененные к отрезку длиной в ^zy/_{x + y}, позволят найти расстояние между первым и вторым пунктами встречи. По условию это расстояние равно ^2z/₉, т. е.

^zyx/_{(x + y)²} = ²/₉z, или ^yx/_{(x + y)²} = ²/₉.

Это уравнение можно переписать так:

2x² − 5ху + 2y² = 0, т. е. 2(^x/_y)² − 5^x/_y + 2 = 0,

откуда

либо ^x/_y = 2, либо ^x/_y = ½. (7)

Очевидно, что эти отношения дают симметричные решения. Если предположить, что скорость автомобиля больше скорости мотоцикла, то x = 2y.

Используем оставшиеся условия задачи. Если бы скорость автомобиля была на 20 км/ч меньше, т. е. равнялась бы (x − 20) км/ч, то первая встреча произошла бы через 3 ч после начала движения. Получаем уравнение

^z/_{x + y − 20} = 3. (8)

Мотоцикл до встречи преодолел бы в этом случае расстояние в 3y км, а расстояние между пунктами первой и второй встреч составило бы ^3yx/_{x + y − 20}. Получаем третье уравнение:

^{3y(x − 20)}/_{x + y − 20} = 60. (9)

Подставим в это уравнение x = 2y. Получим квадратное уравнение, корнями которого являются

y₁ = 20 + 10√2, y₂ = 20 − 10√2.

Второе значение не подходит, так как тогда x₂ < 20.

Итак,

y = (20 + 10√2) км/ч, x = (40 + 20√2) км/ч,

а из уравнения (8) найдем z = (120 + 90√2) км.

Ответ. (120 + 90√2) км.

18.13. Пусть пассажир опоздал на поезд на t ч, проехал на такси x км, а на автобусе y км. Скорость поезда обозначим через u. Тогда путь до встречи с поездом пассажир проедет за

ч, а поезд пройдет этот путь за ^{x + y}/_u ч. Учтя опоздание пассажира, получим

Поездка на такси и автобусе обошлась пассажиру в (ax + А) p. Если бы он ехал все время на такси, то это стоило бы (ax + А − В) p. и он догнал бы поезд, проехав ^{ax + А − В}/_a км. Приравнивая времена, за которые этот путь прошел поезд и проехал догонявший его пассажир, получим второе уравнение:

Третье уравнение очевидно:

Записав его в виде

найдем

Приравниваем выражения для t из уравнений (10) и (11). Получим

т. е.

Поскольку y уже найден, можно вычислить u:

Чтобы задача имела решение, скорость поезда должна быть положительной. Так как v₁ > v₂ и А > В, то из неравенства

следует, что

Ответ.

18.14. Обозначим скорость товарного поезда до остановки через x, расстояние AB через y, а расстояние AC через z. Тогда пассажирский поезд шел вначале со скоростью mx, а после остановки оба поезда шли соответственно со скоростями ^5x/₄ и ^5mx/₄. Весь путь без остановки товарный поезд прошел бы за ^y/_x ч. Поскольку он сделал остановку на t ч в z км от А, а затем прошел оставшиеся (y − z) км со скоростью ^5x/₄, то он прошел весь путь за

^z/_x + ^{4(y − z)}/_5x + t ч.

Следовательно,

^y/_x + t₁ = ^z/_x + ^{4(y − z)}/_5x + t.

Аналогичное уравнение составляем для пассажирского поезда, который шел в обратном направлении:

^y/_mx + t₂ = ^{y − z}/_mx + ^4y/_5mx + t.

Чтобы ответить на вопрос задачи, нужно из времени, за которое товарный поезд прошел отрезок AC, вычесть время, за которое пассажирский поезд прошел расстояние BC. В наших обозначениях эта разность запишется так:

^z/_x − ^{y − z}/_mx.

Именно это выражение нам нужно определить с помощью полученных выше уравнений. Мы может добиться этого, решив уравнения относительно ^z/_x и ^y/_x. После простых преобразований система примет вид

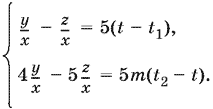
Умножив первое уравнение на −4 и сложив со вторым, найдем ^z/_x, а умножив его на −5 и сложив со вторым, найдем ^y/_x:

^y/_x = 25(t − t₁) − 5m(t₂ − t), ^z/_x = 20(t − t₁) − 5m(t₂ − t).

Остается подставить найденные значения в выражение

(m + 1)^z/_mx − ^y/_mx.

Ответ. ⁵/_m[(4m − 1)(t − t₁) − m²(t₂ − t)].

18.15. Обозначим скорость самолета через x, а скорость вертолета через y. До первой встречи вертолет летел ^d/_y ч, а самолет — ^d/_x ч. Так как самолет вылетел на t ч позднее, то

^d/_y = ^d/_x + t.

Второе уравнение мы получим из условия второй встречи. Вертолет к этому моменту находился в d км от В и пробыл в полете ^{s − d}/_y ч. Самолет, преодолев расстояние s + d, пробыл в полете ^{s + d}/_x ч. Следовательно,

^{s − d}/_y = ^{s + d}/_{x + t}.

Хотя полученную систему уравнений можно решить, а затем ответить на вопрос задачи, мы сначала вычислим интересующую нас величину в предположении, что x и y известны. Вертолет прилетел в В через ^s/_y ч после вылета. Самолет вернулся в А через (t + ^2s/_x) ч после того, как вертолет вылетел из А. Нас интересует величина

t + ^2s/_x − ^s/_y

— на столько позднее самолет вернулся в А, чем вертолет прилетел в В. Таким образом, из полученных уравнений нужно определить ¹/_x и ¹/_y. Умножив первое уравнение на d − s, а второе на d и сложив, найдем

^{(s + d)d}/_x + ^{d(d − s)}/_x + t(d − s) + td = 0, т. е. ^2d²/_x = t(s − 2d),

откуда

¹/_x = ^{t(s − 2d)}/_2d².

Из первого уравнения определяем ¹/_y:

¹/_y = ¹/_x + ^t/_d = ^ts/_2d².

Следовательно,

t + ^2s/_x − ^s/_y = t + ^{2st(s − 2d)}/_2d² − ^ts²/_2d² = t + ^{st(s − 4d)}/_2d².

Задача имеет решение, если все участвующие компоненты положительны. Чтобы величина ¹/_x имела смысл, необходимо s > 2d.

По условию вертолет прилетел в В раньше, чем самолет вернулся в А. Поэтому

t + ^{st(s − 4d)}/_2d² > 0, т. е. s² − 4sd + 2d² > 0.

Получаем квадратное неравенство относительно отношения ^s/_d:

(^s/_d)² − 4^s/_d + 2 > 0,

откуда

^s/_d < 2 − √2 или ^s/_d > 2 + √2.

Первое решение придется отбросить, так как тогда s < 2d − √2 d, а это противоречит условию, что s > 2d.

Ответ. t + ^{st(s − 4d)}/_2d², s > (2 + √2)d.

18.16. Устье реки, на которой стоит порт M, обозначим через А, а устье второй реки — через В. Расстояние MA обозначим буквой x, а расстояние BN — буквой y. Искомое расстояние тогда будет равно s − (x + y). Путь от M до N пароход прошел за:

ч — путь по первой реке (по течению), ^{s − (x + y)}/_v ч — путь по озеру и

ч — путь по второй реке (против течения). Так как весь путь пароход прошел за t ч, то получаем уравнение

Аналогично для пути от N до M получим уравнение

Приравнивая левые части этих уравнений, получим

т. е.

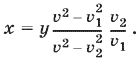
Подставим найденное выражение для x в первое уравнение и найдем

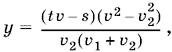
следовательно,

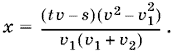
Остается найти s − (x + y).

Ответ.

18.17. Примем расстояние AB за единицу. Пусть скорости пассажирского, курьерского и скорого поездов равны v, 2v и u соответственно (в долях этой единицы).

Тогда время, которое находились в пути до встречи скорый и курьерский поезда, равно ¹/_{u + 2v}, а время до встречи скорого и пассажирского будет равно ¹/_{u + v}. По условию

¹/_{u + 2v} ≥ 10½ − 8 = ⁵/₂, (13)

¹/_{u + v} − ¹/_{u + 2v} ≥ 1. (14)

Нам известно также, что скорый поезд преодолевает расстояние AB за 55 ч. Следовательно, за 1 ч он проходит ⁶/₃₅ AB, т. е. u = ⁶/₃₅. Подставим это значение u в каждое из предыдущих неравенств, находим, что, с одной стороны, v ≤ ⁴/₃₅, а, с другой стороны, ⁴/₃₅ ≤ v ≤ ⁹/₇₀. Обоим неравенствам удовлетворяет единственное значение v = ⁴/₃₅, т. е. пассажирский поезд находился в пути из В в А 8 ч 45 мин и прибыл в А в 16 ч 45 мин.

Полезно обратить внимание на то обстоятельство, что решение системы неравенств, казалось бы, упростится, если неравенства (13) и (14) сложить и заменить их суммой второе неравенство. Однако система неравенств

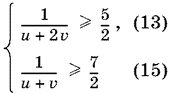
оказывается неравносильной первоначальной системе. Неравенство (15) является следствием системы (13), (14), но заменять им произвольное из исходных неравенств мы не имеем права. Система (13), (15) имеет решение v ≤ ⁴/₃₅, в то время как решение первоначальной системы v = ⁴/₃₅.

Ответ. 16 ч 15 мин.

18.18. Пересылка одной детали в каждом из трех комплектов обходится соответственно в ²/₇, ¼ и ⁷/₂₅ p., т. е. после приведения к общему знаменателю: ²⁰⁰/₇₀₀, ¹⁷⁵/₇₀₀, ¹⁹⁶/₇₀₀ p. Самой дешевой оказывается пересылка в комплектах по 40 деталей. Однако 1100 на 40 не делится и поэтому придется заказывать не только самые выгодные комплекты. Чтобы потерять как можно меньше, мы будем постепенно отказываться от самых выгодных условий, т. е. рассмотрим случаи, когда в комплекты по 40 штук укомплектованы 1080, 1040, 1000, 960, 920, ... деталей. Первый и второй случаи оказываются неосуществимыми, так как мы не сможем получить оставшиеся детали в надлежащих комплектах. Третий случай вполне допустим: он предполагает, что прибудет 25 комплектов по 40 деталей и 4 комплекта по 25 деталей. Таким образом, пересылка обойдется в 25 · 10 + 7 · 4 = 278 p. Любой другой вариант, как легко видеть, приведет к бо́льшим расходам, поскольку количество самых выгодных комплектов уменьшится за счет увеличения количества менее выгодных комплектов (по 25 деталей) или за счет появления самых невыгодных комплектов (по 70 деталей).

Ответ. 25 комплектов по 40 деталей и 4 комплекта по 25 деталей.