Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Задачи
Суммирование
При решении задач, связанных с последовательностями, приходится доказывать утверждения такого типа: «Для любого целого n ≥ p (где p — целое) справедливо...»
Доказательство этих утверждений базируется на аксиоме индукции.
Пусть для некоторого утверждения А доказаны две теоремы.
Теорема 1. Утверждение А справедливо для n = p.
Теорема 2. Из условия, что утверждение А справедливо для всех p ≤ n ≤ k, следует, что оно справедливо для n = k + 1.
Тогда в качестве аксиомы (она называется аксиомой индукции) принимают, что утверждение А справедливо для всех n ≥ p (n, p и А — целые числа).
Метод доказательства, основанный на использовании аксиомы индукции, называется методом математической индукции.
С помощью метода математической индукции можно доказать формулы
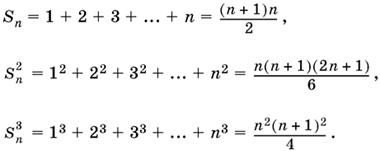
20.1. Докажите неравенство
![]()
20.2. В арифметической прогрессии а1, а2, ..., аn первый член равен разности прогрессии: а1 = d. Считая число n данным, найдите
![]()
20.3. Найдите сумму
![]()
20.4. Найдите зависимость между натуральными n и А, если
![]()
где а ≠ 0, 1, −1.
20.5. Найдите коэффициент при хn в разложении
(1 + x + 2х² + ... + пхn)².
20.6. Решите неравенство
|x − 2х² + 4х³ − 8х4 + ... + (−2)n − 1хn + ...| < 1.
20.7. Найдите сумму
Sn = 1 · 1! + 2 · 2! + 3 · 3! + ... + n · n!.
20.8. Найдите сумму
Sn = x + 4х³ + 7х5 + 10х7 + ... + (3n − 2)х2n − 1.
20.9. Найдите сумму
Sn4 = 14 + 24 + 34 + ... + n4,
считая известными формулы для Sn, Sn², Sn³ (см. с. 103).
20.10. Натуральные числа разбиты на группы
(1), (2, 4), (3, 5, 7), (6, 8, 10, 12), (9, 11, 13, 15, 17), ...
Найдите сумму чисел в n-й группе.
20.11. Вычислите выражение
![]()
20.12. Найдите сумму
1 + 2 · 2 + 3 · 2² + ... + 100 · 299.
20.13. Найдите сумму ряда
![]()