Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Итоги контрольной работы - урок 7 - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА
Цели: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.
Ход урока
I. Сообщение темы и целей урока
II. Итоги контрольной работы
1. Распределение работ по вариантам и результатам решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).
№ задачи Итоги |
1 |
2 |
3 |
... |
6 |
+ |
5 |
||||
± |
1 |
||||
— |
1 |
||||
Ø |
1 |
Обозначения:
+ — число решивших задачу правильно или почти правильно.
± — число решивших задачу со значительными ошибками; .
— — число не решивших задачу;
Ø — число не решавших задачу. Вариант 1, 2 — 8 учеников.
2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, сделавшими эту задачу).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям вариантов и разбор наиболее трудных вариантов).
III. Ответы и решени.
Вариант 1
1. Ответ: (1,8; +∞).
2. Ответ: [-1; 1].
3. Ответ: (-1/3; 3/2].
4. Ответ: (6,6; 6,9).
5. Ответ: (0,5; +∞).
6. Ответ: (-∞; 0,5].
Вариант 2
1. Ответ: (-∞; 1,6).
2. Ответ: [-1; 3].
3. Ответ: (-1/2; 4/3].
4. Ответ: (6,0; 6,3).
5. Ответ: (-∞; 0,6).
6. Ответ: (-∞; 2/3].
Вариант 3
1. Ответ: доказано.
2. Ответ: (-∞; -91).
3. Ответ: [1; 5].
4. Ответ: (2; 4,5].
5. Ответ: (1,4; 2,4).
6. Ответ: при a ∈ (-∞; -1) x ∈ (-∞; a-1], при a = -1 х ∈ (-∞; +∞), при a ∈ (-1; ∞) х ∈ [a-1; ∞).
Вариант 4
1. Ответ: доказано.
2. Ответ: (-88; +∞).
3. Ответ: [-1; 5].
4. Ответ: (1; 2,5].
5. Ответ: (3,8; 4,5).
6. Ответ: при a ∈ (-∞; -1) x ∈ (-∞; a+1], при a = 1 х ∈ (-∞; +∞), при a ∈ (1; +∞) х ∈ [a+1; +∞).
Решения
Вариант 5
1. Учтем, что при всех значениях у величина 3х2 + 2 > 0. По свойству неравенств разделим обе части данного неравенства на эту величину (при этом знак неравенства сохраняется). Получим: ![]() или
или ![]() или 8х < -1, откуда х < -1/8, т. е. x ∈ (-∞; -1/8).
или 8х < -1, откуда х < -1/8, т. е. x ∈ (-∞; -1/8).
Ответ: x ∈ (-∞; -1/8).
2. Неравенство |2 – 7x| ≥ 1 равносильно совокупности неравенств: 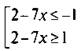 или
или  или
или 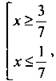 x ∈ (-∞; 1/7]U[3/7; +∞).
x ∈ (-∞; 1/7]U[3/7; +∞).
Ответ: (-∞; 1/7]U[3/7; +∞).
3. Область определения функции задается системой неравенств:  или
или ![]() или
или  т. е. x ∈ (-2/5; 3/4].
т. е. x ∈ (-2/5; 3/4].
Ответ: (-2/5; 3/4].
4. Найдем решение уравнения 4х = aх - 3 или 3 = (а - 4)х, откуда ![]() Так как решения уравнения положительны, то получаем неравенство:
Так как решения уравнения положительны, то получаем неравенство: ![]() или а – 4 > 0. Решение этого неравенства а ∈ (4; +∞).
или а – 4 > 0. Решение этого неравенства а ∈ (4; +∞).
Ответ: (4; +∞).
5. Неравенство |y + 2x| ≤ 1 равносильно двойному неравенству -1 ≤ у + 2х ≤ 1. Вычтем из всех частей неравенства 2х и получим -1 - 2х ≤ у ≤ 1 - 2х.
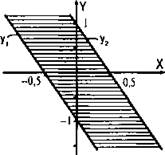
Построим две граничные прямые у1 = -1 - 2х и у2= 1 - 2х. Подставив координаты начала координат, видим, что неравенству удовлетворяют точки, лежащие между и на прямых у1 и у2 (эта область заштрихована).
Ответ: см. график.
6. Разложим правую часть неравенства на множители и получим ![]() Рассмотрим три случая.
Рассмотрим три случая.
а) Если а + 2 < 0 (т. е. а < -2), то разделим обе части данного неравенства на отрицательную величину а + 2 (при этом знак неравенства меняется на противоположный) и получаем х ≤ а - 3.
б) Если а + 2 = 0 (т. е. а = -2), то делить на нулевой множитель нельзя. Подставив значение а = -2 в данное неравенство, получим 0 · х > 0. Очевидно, что такое неравенство выполняется при всех jc, т. е. х ∈ (-∞; +∞).
в) Если а + 2 > 0 (т. е. а > -2), то разделим обе части на положительную величину а + 2 (при этом знак неравенства сохраняется) и получаем х ≥ а - 3. Теперь выпишем ответ в порядке возрастания параметра а.
Ответ: при а ∈ (-∞; -2) х ∈ (-∞; а-3], при а = -2 х ∈ (-∞; +∞), при а ∈ (-2; +∞) х ∈ [а-3; +∞).
Вариант 6
1. Учтем, что при всех значениях .у величина 2х2 + 3 > 0. По свойству неравенств разделим обе части данного неравенства на эту величину (при этом знак неравенства сохраняется). Получим: ![]() или
или ![]() или х < 1 ,т. е. х ∈ (-∞; 1).
или х < 1 ,т. е. х ∈ (-∞; 1).
Ответ: (-∞; 1)..
2. Неравенство |3 - 5х| ≥ 2 равносильно совокупности неравенств: 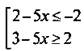 или
или  или
или 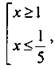 т. е. x ∈ (-∞; 1/5]U[1; +∞).
т. е. x ∈ (-∞; 1/5]U[1; +∞).
Ответ: (-∞; 1/5]U[1; +∞).
I 5J
3. Область определения функции задается системой неравенств: 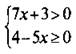 или
или ![]() или
или  т. е. x ∈ (-3/7; 4/5].
т. е. x ∈ (-3/7; 4/5].
Ответ: (-3/7; 4/5].
4. Найдем решение уравнения 3х = ах - 7 или 7 = (а - 3)х, откуда ![]() Так как решения уравнения отрицательны, то получаем неравенство:
Так как решения уравнения отрицательны, то получаем неравенство: ![]() или а – 3 < 0. Решение этого неравенства a ∈ (-∞; 3).
или а – 3 < 0. Решение этого неравенства a ∈ (-∞; 3).
Ответ: (-∞; 3).
5. Неравенство |y - 3х| ≤ 2 равносильно двойному неравенству -2 ≤ у - 3х ≤ 2. Прибавим ко всем частям неравенства 3х и получим 3х – 2 ≤ y ≤ 3х + 2.
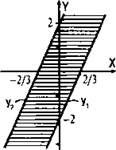
Построим две граничные прямые у1 = 3х - 2 и у2 = 3х + 2. Подставив координаты начала координат, видим, что неравенству удовлетворяют точки, лежащие между, и на прямых у1 и у2 (эта область заштрихована).
Ответ: см. график.
6. Разложим правую часть неравенства на множители и получим ![]() Рассмотрим три случая.
Рассмотрим три случая.
а) Если а + 3 < 0 (т. е. а < -3), то разделим обе части данного неравенства на отрицательную величину а + 3 (при этом знак неравенства меняется на противоположный) и получаем х ≥ а - 2.
б) Если а + 3 = 0 (т. е. а = -3), то делить на нулевой множитель нельзя. Подставив значение а = -3 в данное неравенство, получим 0 · х ≤ 0. Очевидно, что такое неравенство выполняется при всех x, т. е. х ∈ (-∞; +∞).
в) Если а + 3 > 0 (т. е. а > -3), то разделим обе части на положительную величину а + 3 (при этом знак неравенства сохраняется) и получаем х ≤ а - 2.
Теперь выпишем ответ в порядке возрастания параметра а.
Ответ: при а ∈ (-∞; -3) х ∈ (a-2; +∞], при а = -3 х ∈ (-∞; +∞), при а ∈ (-3; +∞) х ∈ [-∞; a-2).