Решение более сложных неравенств - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА

Цель: рассмотреть решение более сложных неравенств.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Решите аналитически неравенство:

2. Решите графически неравенство:

Вариант 2

1. Решите аналитически неравенство:

2. Решите графически неравенство:

III. Изучение нового материала (основные понятия)

Сначала рассмотрим более сложные линейные неравенства. Как правило, эта сложность связана или с громоздкостью примеров, или с наличием в них параметров.

Пример 1

Решим неравенство

В данном примере основная сложность связана с громоздкостью левой части неравенства. Поэтому выполним ее преобразования, раскрывая постепенно скобки (начиная с самых внутренних) и приводя подобные члены. Получаем: или 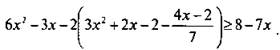Внутри скобок приведем выражения к общему знаменателю. Имеем: или Умножим все члены неравенства на положительное число 7 (при этом знак неравенства сохраняется): или - Члены неравенства, зависящие от х, перенесем в левую часть, а числа — в правую часть. Имеем: или 8х ≥ 32. Разделим обе части неравенства на положительное число 8 (знак неравенства сохраняется) и получим х ≥ 4, т. е. х ∈ [4; +∞).

Пример 2

Решим неравенство

Для нахождения решения неравенства необходимо обе его части разделить на выражение а - 1, зависящее от параметра а. Однако это выражение при различных значениях а будет иметь разный знак. Поэтому надо рассмотреть три случая.

а) Если а - 1 < 0 (т. е. а < 1).

Тогда при делении обеих частей данного неравенства на отрицательное выражение а - 1 знак неравенства меняется на противоположный. Находим или х ≥ а + 1 или х ∈ [а+1; +∞). Итак, в этом случае получили: при а ∈ (-∞; 1) х ∈ [а+1; +∞).

б) Если а - 1 = 0 (т. е. а = 1).

В этом случае коэффициент при х равен 0. Поэтому делить обе части данного неравенства на выражение а - 1 нельзя (еще раз подчеркнем, что в этом случае такое выражение равно нулю). Тогда подставим значение a = 1 в данное неравенство (a – 1)x ≤ a2 - 1 и получим 0 · х ≤ 0. При любом значении х из этого неравенства имеет верное числовое неравенство 0 ≤ 0. Следовательно, в этом случае решением данного неравенства является любое число х. Итак, при а = 1 х ∈ (-∞; +∞).

в) Если а - 1 > 0 (т. е. а > 1).

Тогда при делении обеих частей данного неравенства на положительное выражение a - 1 знак неравенства сохраняется. Находим или х ≤ а + 1 или х ∈ (-∞; а+1].

Так как в задачах с параметрами очень важна запись ответа (ответ записывается в порядке возрастания параметра), то приведем полный ответ:

При а ∈ (-∞; 1) х ∈ [а+1; +∞); при а = 1 х ∈ (-∞; +∞); при а ∈ (1; +∞) х ∈ (-∞; а+1].

Разумеется, к неравенствам с параметрами приводят и более сложные задачи.

Пример 3

При каких значениях параметра а уравнение aх2 + х - 1 = 0 не имеет решений?

Так как старший коэффициент уравнения а зависит от параметра а, то необходимо рассмотреть два случая.

а) Если а ≠ 0, то данное уравнение ах2 + х - 1 = 0 является квадратным. Такое уравнение не имеет решений, если его дискриминант D = 1 + 4a < 0. Решение этого неравенства а ∈ (-∞; -1/4). Заметим, что в указанный промежуток значение а = 0 не входит.

б) Если а = 0, то данное уравнение ах2 + х - 1 = 0 является линейным и имеет вид x – 1 = 0. Очевидно, что это уравнение имеет единственное решение х = 1.

Итак, при а ∈ (-∞; -1/4) данное уравнение решений не имеет.

Пример 4

При каких значениях параметра а оба корня уравнения меньше 5?

Прежде всего решим данное квадратное уравнение. Найдем его дискриминант и корни т. е. х1 = 3 и х2 = 1 - а. Очевидно, что корень х1 уже удовлетворяет условию х1 < 5. Второй корень х2 должен также удовлетворять аналогичному неравенству. Получаем неравенство 1 – а < 5, решение которого а > -4 , т. е. а ∈ (-4; +∞).

Теперь необходимо добиться, чтобы данное уравнение имело два корня (имеется в виду два различных корня). Получаем условие 3 ≠ 1 - а, откуда а ≠ -2. Учитывая выше написанное, имеем, что при а ∈ (-4; -2)U(-2; +∞) оба корня данного уравнения меньше 5.

Теперь рассмотрим линейные неравенства с двумя переменными. Как правило, подобные задачи сводятся к изображению множества точек, координаты которых удовлетворяют неравенству, на координатной плоскости.

Пример 5

На координатной плоскости изобразим множество точек, координаты которых удовлетворяют неравенству у - 2 ≥ х - 3.

Запишем данное неравенство в виде у ≥ х - 1. Сначала построим график линейной функции у = х - 1 (прямая линия). Эта линия разделяет все точки координатной плоскости на точки, расположенные над этой прямой, и точки, расположенные под этой прямой.

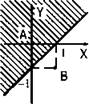
Проверим, какие точки удовлетворяют данному неравенству.

Из первой области возьмем, например, контрольную точку A (0; 0) — начало координат. Легко проверить, что тогда неравенство у ≥ х - 1 выполняется. Из второй области выберем, например, контрольную точку В (1; -1). Для такой точки неравенство у ≥ х - 1 не выполняется. Следовательно, данному неравенству удовлетворяют точки, расположенные выше и на прямой у = х - 1 (т. е. точки, аналогичные точке А). Эти точки заштрихованы.

Обратимся теперь к рассмотрению нелинейных неравенств. Достаточно часто такая нелинейность связана с наличием знаков модулей в неравенстве. Решают подобные неравенства аналитически (раскрывая знаки модулей) или графически.

Пример 6

Решим неравенство |х - 1| < 3.

Сначала решим это неравенство аналитически, рассмотрев два случая.

а) Если x – 1 ≥ 0 (т. е. х ≥ 1), то |х - 1| = х - 1 и неравенство имеет вид x - 1 < 3. Решение этого неравенства х < 4. Учитывая условие х ≥ 1, получаем в этом случае решение 1 ≤ х < 4 или х ∈ [1; 4).

б) Если х - 1 < 0 (т. е. х < 1), то |х - 1| = -х - 1 = 1 - х и неравенство имеет вид 1 - х < 3. Решение этого неравенства -2 < х. Учитывая условие х < 1, получаем в этом случае решение -2 < х < 1 или х ∈ (-2; 1).

Находим объединение полученных решений [1; 4) и (-2; 1) и получаем окончательный ответ: х ∈ (-2; 4).

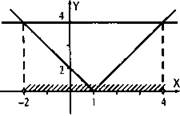
Теперь решим неравенство |х - 1| < 3 графически. Построим графики функций у1 = |х - 1| (он получается смещением графика функции у = |х| на одну единицу вправо) и у2 = 3 (горизонтальная прямая). Неравенство |х - 1| < 3 означает, что надо найти такие значения х, при которых значения функции у1 меньше значений функции у2 (или график функции у1 лежит ниже графика функции у2. Из рисунка видно, что такие х лежат в промежутке (-2; 4).,

Пример 7

Решим неравенство |х - 1| - |х + 2| ≤ -2.

Решим такое неравенство аналитически, раскрывая знаки модулей методом интервалов. Выражение х - 1 меняет знак при х = 1, выражение х + 2 — при х = -2. Нанеся эти значения х на числовую ось, получаем три числовых промежутка (интервала).

1) Если х ∈ (-∞; -2], то х - 1 < 0 и |x - 1| = -(x - 1) = 1 - x; х + 2 ≤ 0 и |х + 2| = -(х + 2)= -х - 2. Тогда данное неравенство имеет вид: 1 – х - (-х - 2) ≤ -2 или 3 < -2. Так как получили неверное неравенство, то ни одна точка рассматриваемого промежутка (-∞; -2] не удовлетворяет данному неравенству.

2) Если х ∈ (-2; 1), то х - 1 < 0 и |x - 1| = -(x - 1) = 1 - x; х + 2 > 0 и |х + 2| = х + 2. Тогда данное неравенство имеет вид: 1 – х - (х + 2) ≤ -2 или -2х - 1 ≤ -2. Решение этого неравенства х ≥ 1/2. С учетом рассматриваемого промежутка (-2; 1) получаем решение х ∈ [1/2; 1).

3) Если х ∈ [1; +∞), то х - 1 ≥ 0 и |х - 1| = х - 1; х + 2 > 0 и |х + 2| = х + 2. Тогда данное неравенство имеет вид: х – 1 - (х + 2) ≤ -2 или -3 ≤ -2. Так как получили верное неравенство, то все точки рассматриваемого промежутка x ∈ [1; +∞) являются решениями данного неравенства.

Находим объединение полученных решений [1/2; 1) и [1; +∞) и получаем окончательный ответ: х ∈ [1/2; +∞).

К нелинейным неравенствам также приводят члены, содержащие переменную в степени выше первой.

Пример 8

Решим неравенство |х + 1| + х2 + 2х + 1 ≤ 0.

Запишем неравенство в виде |х + 1| + (х + 1) ≤ 0 и введем новую переменную t = х + 1. Тогда неравенство принимает вид |t| + t2 ≤ 0. Так как |t| ≥ 0 и t2 ≥ 0 при всех значениях t, то сумма |t| + t2 ≥ 0 при всех t. Поэтому неравенство |t| + t2 ≤ 0 имеет единственное решение t = 0. Теперь вернемся к старой неизвестной х. Получаем линейное уравнение х + 1 = 0, решение которого х = -1. Итак, решение данного неравенства х = -1.

Подобного типа неравенства существуют и с двумя переменными.

Пример 9

Решим неравенство

Аналогично предыдущему примеру, при всех значениях x и у выражения (х - 2у +1)2 ≥ 0 и |3x + y - 2| ≥ 0. Поэтому сумма Следовательно, данное неравенство выполняется только при тех значениях х и у, которые являются решением линейной системы уравнений Решим эту систему, например, способом подстановки. Из второго уравнения выразим у = 2 - 3х и подставим в первое уравнение. Получаем: x - 2(2 - 3х) + 1 = 0 или х - 4 + 6x + 1 = 0, или 7х = 3, откуда x = 3/7. Используя равенство у = 2 - 3х, найдем Итак, данное неравенство имеет единственное решение: x = 3/7, y = 5/7.

Достаточно часто на координатной плоскости приходится изображать множество точек, удовлетворяющих нелинейному неравенству.

Пример 10

На координатной плоскости изобразим множество точек, координаты которых удовлетворяют неравенству у - 1 ≤ х2.

Запишем неравенство в виде у ≤ х2 + 1 и построим параболу у = х2 + 1 (этот график получается смещением графика у = х2 на одну единицу вверх). Парабола разбивает точки плоскости на точки, расположенные над параболой, и точки, расположенные под параболой. Взяв в качестве контрольной точки начало координат (аналогично примеру 5), получаем верное неравенство 0 ≤ 1. Поэтому данному неравенству удовлетворяют точки, расположенные ниже параболы и на параболе. Эти точки заштрихованы.

IV. Задание на уроке и дома

1. Аналитически решите неравенство:

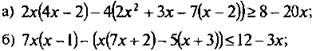
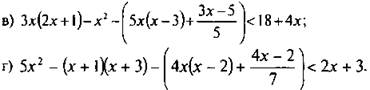
Ответы:

2. При всех значениях параметра а решите неравенство:

Ответы: а) при а ∈ (-∞; -3) х ∈ (-∞; a-3], при a = -3 х ∈ (-∞; +∞), при а ∈ (-3; +∞) х ∈ [а-3; +∞);

б) при a ∈ (-∞; 2) х ∈ [-a-2; +∞), при a = 2 х ∈ (-∞; +∞), при a ∈ (2; +∞) х ∈ (-∞; -а-2];

в) при а ∈ (-∞; 1) х ∈ (а+1; +∞), при а = 1 х ∈ 0, при a ∈ (1; +∞) х ∈ (-∞; а+1);

г) при a ∈ (-∞; -2) х ∈ (-∞; а-2), при a = -2 х ∈ 0, при а ∈ (-2; +∞) х ∈ (а-2; +∞) (указание: примеры в, г привести к виду, аналогичному примерам а, б);

д) при а ≠ 1 при а = 1 х ∈ (-∞; +∞);

е) при а ≠ -2 при а = -2 х ∈ (-∞; +∞);

3. При каких значениях параметра а уравнение:

а) 3х2 - 2х + а = 0 не имеет корней;

б) 2х2 - 3х + 5а = 0 имеет два различных корня;

в) х2 -(a + 4)х + 3х + 3 = 0 имеет один корень, больший 6;

г) х2 - 2ах + 2а - 1 = 0 имеет один отрицательный корень;

д) ах2 - 3х + 2 = 0 имеет хотя бы один корень;

е) 3ах2 - 4х + 1 = 0 имеет два различных корня;

ж) 2х2 - (a + 2)х + 3а- 12 = 0 имеет хотя бы один отрицательный корень;

з) 3х2 - (a + 3)х + 2а – 6 = 0 имеет хотя бы один положительный корень?

Ответы:

4. Решите неравенства:

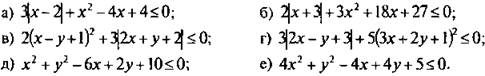
Ответы: а) х = 2; б) x = -3; в) x = -1, y = 0; г) x = -1, у = 1; д) х = 3, y = -1; е) х = 1/2, у = -2 (указание: в примерах д, е выделите полные квадраты суммы и разности величин).

5. На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству:

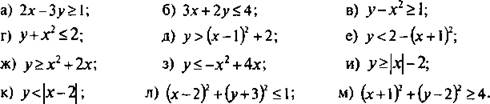
Указание: уравнение окружности с центром в точке А (а; в) и радиуса R имеет вид: (x – a)2 + (y – b)2 = R2.

V. Подведение итогов урока