Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Решение дробных рациональных уравнений - ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: решение дробных рациональных уравнений сведением их к линейным или квадратным уравнениям.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные сведения)
1. Подход к определению типов уравнения.
Пример 1
Рассмотрите уравнения:
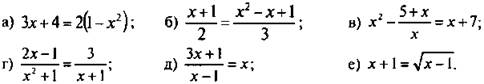
По аналогии с типами алгебраических выражений назовите данные уравнения.
2. Типы алгебраических уравнений
Уравнения, в которых обе части являются рациональными выражениями, называют рациональными уравнениями. В примере 1 рациональными уравнениями являются а-д. Рациональные уравнения, в которых обе части являются целыми выражениями, называют целыми уравнениями. В примере 1 целыми будут уравнения а, б (квадратные уравнения). Рациональное уравнение, в котором хотя бы одна из частей является дробным выражением, называют дробным рациональным уравнением. В примере 1 такими уравнениями являются в-д.
3. Решение рациональных уравнений
Основной способ решения рациональных уравнений состоит в преобразовании их в простейшие целые уравнения: линейные или квадратные.
Пример 2
Решим целое уравнение ![]()
Наименьший общий знаменатель дробей, входящих в уравнение, равен 6. Умножим все члены уравнения на это число 6 и получим равносильное уравнение х2 + 9 – 2 · 2х = х + 3. Перенесем все члены в левую часть и получим равносильное квадратное уравнение х2 - 5х + 6 = 0. Корни этого уравнения х1 = 2 и х2 = 3 являются также и корнями данного уравнения.
Пример 3
Решим дробное рациональное уравнение ![]()
По аналогии с предыдущим примером умножим обе части уравнения на знаменатель 2 - х (при условии, что 2 - х ≠ 0 (т. е. х ≠ 2)) и по свойству уравнений получим равносильное уравнение х2 - 6х + 8 = 2 - х. Перенесем все члены в левую часть и получим равносильное уравнение х2 - 5х + 6 = 0 (при условии, что х ≠ 2). Корни этого квадратного уравнения х1 = 2 и х2 = 3. Однако корнем данного уравнения является только корень х = 3.
Пример 4
Решим дробное рациональное уравнение ![]()
Общий знаменатель дробей, входящих в уравнение, равен (х – 5)(x + 5). Умножим все члены уравнения на это выражение (при условии, что (х – 5)(x + 5) ≠ 0 (т. е. х = ±5)) и получим равносильное уравнение: ![]() или
или ![]() или
или ![]() Перенесем все члены уравнения в левую часть и приведем подобные члены. Получаем равносильное квадратное уравнение х2 + 3х -10 = 0. Корни этого уравнения х1 = -5 и х2 = 2. Условию х ≠ ±5 удовлетворяет только корень х = 2. Поэтому корень данного уравнения х = 2.
Перенесем все члены уравнения в левую часть и приведем подобные члены. Получаем равносильное квадратное уравнение х2 + 3х -10 = 0. Корни этого уравнения х1 = -5 и х2 = 2. Условию х ≠ ±5 удовлетворяет только корень х = 2. Поэтому корень данного уравнения х = 2.
Пример 5
Решим дробное рациональное уравнение ![]()
Разложим знаменатели дробей, входящих в уравнение, на множители ![]() Общий знаменатель этих дробей (2х – 3)(2х + 3)2. Умножим все члены данного уравнения на это выражение (при условии, что оно не равно нулю (т. е. х ≠ ±1,5)) и получим равносильное уравнение:
Общий знаменатель этих дробей (2х – 3)(2х + 3)2. Умножим все члены данного уравнения на это выражение (при условии, что оно не равно нулю (т. е. х ≠ ±1,5)) и получим равносильное уравнение: ![]() или
или ![]() или
или ![]() Перенесем все члены уравнения в правую часть и приведем подобные члены. Получаем равносильное неполное квадратное уравнение: 0 = 4х2 + 24х или 0 = х(х + 6). Оба корня этого уравнения х1 = 0 и х2 = -6 удовлетворяют условию х ≠ ± 1,5 и являются корнями данного уравнения.
Перенесем все члены уравнения в правую часть и приведем подобные члены. Получаем равносильное неполное квадратное уравнение: 0 = 4х2 + 24х или 0 = х(х + 6). Оба корня этого уравнения х1 = 0 и х2 = -6 удовлетворяют условию х ≠ ± 1,5 и являются корнями данного уравнения.
При решении дробных рациональных уравнений целесообразно:
1. Разложить все знаменатели дробей, входящих в уравнение, на множители.
2. Найти общий знаменатель этих дробей.
3. Умножить все члены данного уравнения на общий знаменатель.
4. Решить получившееся целое уравнение.
5. Из корней этого уравнения исключить те, которые обращают в нуль общий знаменатель данного уравнения.
Достаточно часто встречаются дробные рациональные уравнения, содержащие знаки модуля или параметры.
Пример 6
Решим уравнение ![]()
Если модуль некоторой величины равен 2, то сама величина равна ±2. Рассмотрим эти случаи.
а) ![]() Умножим обе части этого уравнения на знаменатель х - 1 и получим: x + 1 = 2(x - 1) или х + 1 = 2х - 2, откуда х = 3. Заметим, что для такого значения х знаменатель дроби х - 1 ≠ 0. Поэтому х = 3 — корень данного уравнения.
Умножим обе части этого уравнения на знаменатель х - 1 и получим: x + 1 = 2(x - 1) или х + 1 = 2х - 2, откуда х = 3. Заметим, что для такого значения х знаменатель дроби х - 1 ≠ 0. Поэтому х = 3 — корень данного уравнения.
б) ![]() Опять умножим обе части этого уравнения на знаменатель х - 1 и получим: х + 1 = -2(х - 1) или х + 1 = -2х + 2, откуда 3х = 1, откуда х = 1/3. При этом знаменатель дроби х - 1 ≠ 0. Значит, х = 1/3 — также корень данного уравнения.
Опять умножим обе части этого уравнения на знаменатель х - 1 и получим: х + 1 = -2(х - 1) или х + 1 = -2х + 2, откуда 3х = 1, откуда х = 1/3. При этом знаменатель дроби х - 1 ≠ 0. Значит, х = 1/3 — также корень данного уравнения.
Пример 7
Решим уравнение ![]()
Используя определение модуля, раскроем знак модуля, рассмотрев два случая.
а) Если х - 2 > 0 (т. е. х > 2), то |х - 2| = х - 2 и уравнение имеет вид ![]() Умножим обе части этого уравнения на х - 2 и получим квадратное уравнение: х2 - 3х = 2(х - 2) или х2 - 5х + 4 = 0. Корни этого уравнения х1 = 1 и х2 = 4. Условию х > 2 удовлетворяет только корень х = 4. Поэтому х = 4 - корень данного уравнения.
Умножим обе части этого уравнения на х - 2 и получим квадратное уравнение: х2 - 3х = 2(х - 2) или х2 - 5х + 4 = 0. Корни этого уравнения х1 = 1 и х2 = 4. Условию х > 2 удовлетворяет только корень х = 4. Поэтому х = 4 - корень данного уравнения.
б) Если х - 2 < 0 (т. е.х< 2), то |х - 2| = -(х - 2) = 2 - х и уравнение имеет вид ![]() Умножим обе части этого уравнения на 2 - х и получим квадратное уравнение: х2 - 3х = 2(2 - х) или х2 – х - 4 = 0. Корни этого уравнения
Умножим обе части этого уравнения на 2 - х и получим квадратное уравнение: х2 - 3х = 2(2 - х) или х2 – х - 4 = 0. Корни этого уравнения ![]() Условию х < 2 удовлетворяет только корень
Условию х < 2 удовлетворяет только корень ![]() Поэтому
Поэтому ![]() - также корень данного уравнения.
- также корень данного уравнения.
Пример 8
Решим уравнение ![]()
Умножим все члены уравнения на общий знаменатель дробей (x + 2)(x - а) (при условии, что х + 2 ≠ 0 и х – а ≠ 0) и получим: ![]() или
или ![]() Перенесем все члены уравнения в правую часть, приведем подобные члены и получим линейное уравнение 0 = 8х + 12 – 2a. Решим это уравнение. Имеем: a - 6 = 4х, откуда
Перенесем все члены уравнения в правую часть, приведем подобные члены и получим линейное уравнение 0 = 8х + 12 – 2a. Решим это уравнение. Имеем: a - 6 = 4х, откуда ![]() .
.
Так как параметр а может принимать любые значения, то найденное решение ![]() может оказаться таким, что х + 2 = 0 или х - а = 0. Найдем, при каких значениях параметра а выполняется хотя бы одно из этих условий.
может оказаться таким, что х + 2 = 0 или х - а = 0. Найдем, при каких значениях параметра а выполняется хотя бы одно из этих условий.
а) ![]() Эта величина
Эта величина ![]() при а = -2.
при а = -2.
б) ![]() Величина
Величина ![]() также при а = -2.
также при а = -2.
Итак, при а ≠ -2 уравнение имеет корень ![]() , при а = -2 уравнение корней не имеет (т. к. при этом знаменатели дробей в данном уравнении равны нулю).
, при а = -2 уравнение корней не имеет (т. к. при этом знаменатели дробей в данном уравнении равны нулю).
Пример 9
При каких значениях параметра а уравнение ![]() имеет единственное решение?
имеет единственное решение?
Данная дробь равна нулю, если ее числитель (а + 4)х2 + 6х - 1 = 0 и при этом знаменатель х + 3 ≠ 0 (т. е. х ≠ -3). Поэтому данное уравнение имеет единственное решение в двух случаях.
а) Если уравнение (а + 4)х2 + 6х - 1 = 0 имеет единственный корень, не равный числу -3. Это возможно в двух случаях:
— если уравнение (а + 4)х2 + 6х - 1 = 0 является линейным. Это возможно, если старший коэффициент уравнения a + 4 = 0, откуда a = -4. Для такого значения а уравнение имеет вид 6х - 1 = 0 и единственный корень х = 1/6 (не равный числу -3);
— если уравнение (а + 4)х2 + 6х - 1 = 0 является квадратным, но имеет один корень. Этот случай возможен при двух условиях: а + 4 ≠ 0 (т. е. а ≠ -4) и дискриминант D = 36 + 4(а + 4) = 0. Решим это уравнение: 9 + а + 4 = 0, откуда а = -13. Это значение а = -13 удовлетворяет и условию а ≠ -4.
б) Если уравнение (а + 4)х2 + 6х - 1 = 0 имеет два корня, но один из этих корней равен числу -3 (и не является решением данного уравнения). Найдем, при каком значении параметра а уравнение (а + 4)х2 + 6х - 1 = 0 имеет корень, равный -3. Подставим значение х = -3 в уравнение (а + 4)х2 + 6х – 1 = 0 и получим: (a + 4) · 9 + 6 · (-3) - 1 = 0, или 9а + 17 = 0, откуда a = -17/9.
При значении а = -17/9 уравнение (a + 4)х2 + 6х - 1 = 0 имеет вид: 19/9х2 + 6х - 1 = 0 или 19х2 + 54x - 9 = 0. Один корень этого уравнения известен х1 = -3. Второй корень найдем, используя теорему Виета х1х2 = -9/19, тогда ![]() Очевидно, что этот корень не равен числу -3.
Очевидно, что этот корень не равен числу -3.
Итак, при а = -4, а = -13 и а = -17/9, данное уравнение имеет единственное решение.
III. Контрольные вопросы
1. Какое уравнение называют рациональным?
2. Определение целого уравнения.
3. Какое уравнение называют дробным рациональным уравнением?
4. Каким уравнением является: а) линейное уравнение; б) квадратное уравнение?
IV. Задание на уроке
№ 590 (в, е); 591 (а, в); 593 (а, б); 595 (б); 596 (а, б); 598 (а, в).
V. Задание на дом
№ 590 (а, б, д); 592 (в, ж); 593 (г, е); 595 (в); 596 (в, г); 599 (в).
VI. Творческие задания
1. Решите уравнение.
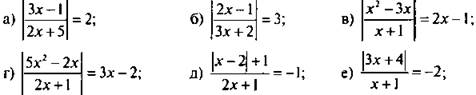
![]()
Ответы:
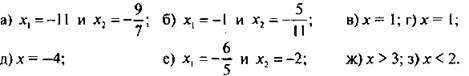
2. При всех значениях параметра а решите уравнение:
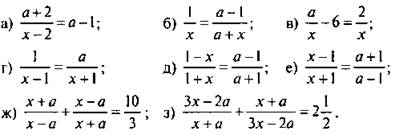
Ответы: а) при а ≠ 2 и а ≠ 1 ![]() при а = -2 или а = 1 решений нет;
при а = -2 или а = 1 решений нет;
б) при a ≠ 0, a ≠ 1 и а ≠ 2 ![]() при а = 0 или а = 1, или a = 2 решений нет;
при а = 0 или а = 1, или a = 2 решений нет;
в) при а ≠ 2 ![]() при а = 2 решении нет;
при а = 2 решении нет;
г) при а ≠ 0 ![]() при а = 0 решении нет;
при а = 0 решении нет;
д) при а ≠ -1 и a ≠ 0 х = 1/a, при а = -1 или а = 0 решений нет;
е) при а ≠ 1 х = -а, при а = 1 решений нет;
ж) при а ≠ 0 х1 = -2а и х2 = 2а , при а = 0 решений нет;
з) при а ≠ 0 х1 = -4а и х2 = a, при а = 0 решений нет.
VII. Подведение итогов урока