Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Графики функций, содержащих модуль - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ
Цель: вспомнить понятие модуля и рассмотреть построение графиков функций, содержащих модуль.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Постройте график функции:
![]()
Вариант 2
Постройте график функции.
![]()
III. Изучение нового материала (основные понятия)
Сначала напомним понятие модуля числа и его основные свойства.
Модулем (абсолютной величиной) действительного числа а называется само это число а, если оно неотрицательно, и противоположное число (-а), если число а отрицательно. Модуль числа а обозначают символом (значком) |а|.
Итак, ![]()
Пример 1
а) |5,6| = 5,6, т. к. число а = 5,6 неотрицательно (и даже положительно);
б) |0| = 0, т. к. число а = 0 неотрицательно;
в) |=2,3| = -(-2,3) - 2,3, т. к. число а = -2,3 отрицательно.
На числовой оси |а| отвечает расстоянию от точки а до точки 0; |а - b| отвечает расстоянию между точками а - b.
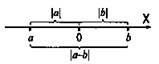
Свойства абсолютных величин чисел:
![]()
Эти свойства легко получаются из определения и геометрического смысла модуля числа а.
Пример 2
Доказать неравенство ![]()
Неравенства легко доказать, используя геометрический смысл модуля числа. Изобразим на числовой оси числа а и b. Тогда |а - b| — расстояние между точками а и b, |а| — расстояние от точки а до точки 0, |b| — расстояние от точки b до точки 0.

Если числа а и b одного знака (рис. а) (т. е. положительные или оба отрицательные), то видно, что ![]() Если числа а и b разных знаков (рис. б) (т. е. одно отрицательное, а другое положительное), то видно, что
Если числа а и b разных знаков (рис. б) (т. е. одно отрицательное, а другое положительное), то видно, что ![]() Объединяя эти два случая, получаем
Объединяя эти два случая, получаем ![]()
Пример 3
Решить уравнение: ![]()
а) Очевидно, что такое уравнение решений не имеет, т. к. расстояние между точками х и 1 не может быть отрицательным.
б) В этом уравнении расстояние между точками х и 1 равно нулю, т. е. точки х и 1 совпадают. Поэтому уравнение имеет единственное решение х = 1.
Это решение легко проверить: ![]()
в) В таком уравнении расстояние между точками х и 1 равно 2, т. е. точках удалена от точки 1 на две единицы. Поэтому или число х меньше числа 1 на две единицы (т. е. х = 1 - 2 = -1) или число х больше числа 1 на две единицы (т. е. х = 1 + 2 = 3). Следовательно, уравнение имеет два решения: х = -1 и х = 3.
Эти решения также легко проверить. Для значения х = -1 получаем: ![]() Для значения х = 3 имеем: |3 - 1| = |2| = 2.
Для значения х = 3 имеем: |3 - 1| = |2| = 2.
Заметим, что возможен и другой способ решения. Если |х - 1| = 2, то сама величина х - 1 может равняться или 2, или -2. Получаем два линейных уравнения: х - 1 = 2 (его корень х = 3) и х - 1 = -2 (корень х = -1).
Перейдем теперь к рассмотрению графиков функций, содержащих модуль.
Пример 4
Построить график функции у = |х - 1|.
Так как в формулу функции входит модуль, то его необходимо раскрыть, рассмотрев два случая. В этом примере а = х - 1. Поэтому функцию можно записать в виде 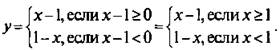 .
.
Поэтому построим график функции у = х - 1 и выберем из него луч АВ, точки которого удовлетворяют условию х ≥ 1. Также строим график линейной функции у = 1 - х и выберем из него луч АС, точки которого удовлетворяют условию х < 1. Таким образом, графиком данной функции является ломаная САВ.
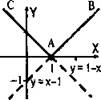
Пример 5
Построить график функции у = |х| — х + 1.
Так как в эту функцию входит |х|, то необходимо рассмотреть два случая.
а) Если х ≥ 0, то |х| = х и получаем у = х - х + 1 = 1 или у = 1. Строим прямую у = 1 для неотрицательных значений х (х ≥ 0).
б) Если х < 0, то |х| = -х и получаем у = -х – х + 1 = -2х + 1 или у = -2х + 1. Для отрицательных х (х < 0) строим прямую у = -2х + 1. В результате получаем график данной функции, состоящий из лучей а и b.

Пример 6
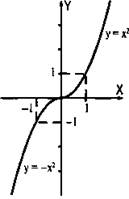
Построить график функции у = x|x|.
Вновь раскроем |х|, рассмотрев два случая.
а) Если х ≥ 0, то |х| = x и функция имеет вид у = х · x = х2. Построим параболу у = х2 для неотрицательных значений х (т. е. х ≥ 0).
б) Если х < 0, то |х| = -х и функция имеет вид у = х · (-х) = -х2. Строим параболу у = -х2 для отрицательных значений х (т. е. х < 0).
Пример 7
Построить график функции ![]()
Величина а = х + 1, стоящая под знаком модуля, может быть как положительной, так и отрицательной (нулю эта величина равняться не может). Поэтому по определению модуля запишем функцию в виде 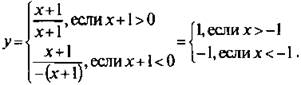 Строим прямую с уравнением у = 1 для х > -1 и прямую у = -1 для х < -1.
Строим прямую с уравнением у = 1 для х > -1 и прямую у = -1 для х < -1.
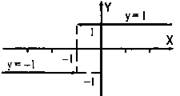
В точке х = -1 функция не определена. Поэтому точки графика, для которых х = -1, указаны стрелками (эти точки в график не входят).
Пример .
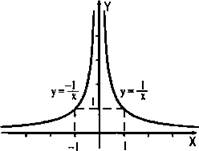
Построить график функции y = 1/|x|.
Можно построить этот график, пользуясь определением модуля. Получаем 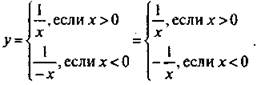 Поэтому для положительных значений х строим ветвь гиперболы у = 1/x, для отрицательных значений х построим ветвь гиперболы у = -1/x.
Поэтому для положительных значений х строим ветвь гиперболы у = 1/x, для отрицательных значений х построим ветвь гиперболы у = -1/x.
Значительно проще построить график этой функции, если использовать понятие о четности (нечетности) функций. Предварительно введем еще одно понятие — симметричность области определения функции. Область определения называется симметричной, если функция определена и в точке х0, и в точке (-х0) (т. е. в точке симметричной х0 относительно начала числовой оси).
Пример 9
а) Областью определения функции ![]() являются все значения х, кроме тех, для которых х2 - 1 = 0 (т. е. х = ±1). Поэтому эта функция определена, например, как при х = -3, так и при х = -(-3) = 3. И наоборот, эта функция не определена и при х = -1, и при х = -(-1) = 1 .Следовательно, область определения данной функции (всех, кроме х = ± 1) — симметрична.
являются все значения х, кроме тех, для которых х2 - 1 = 0 (т. е. х = ±1). Поэтому эта функция определена, например, как при х = -3, так и при х = -(-3) = 3. И наоборот, эта функция не определена и при х = -1, и при х = -(-1) = 1 .Следовательно, область определения данной функции (всех, кроме х = ± 1) — симметрична.
б) Областью определения функции ![]() являются все значения х, кроме тех, для которых х - 1 = 0 (т. е. х = 1). Поэтому эта функция определена в точке х = -1, но не определена в симметричной точке х = -(-1) = 1. Итак, область определения данной функции не симметричная.
являются все значения х, кроме тех, для которых х - 1 = 0 (т. е. х = 1). Поэтому эта функция определена в точке х = -1, но не определена в симметричной точке х = -(-1) = 1. Итак, область определения данной функции не симметричная.
Понятие четности функции вводится только для функции с симметричной областью определения. Функция называется четной, если при изменении знака аргумента значение функции не меняется, т. е. y(-х) = у(х). График четной функции всегда симметричен относительно оси ординат.
Функция называется нечетной, если при изменении знака аргумента значение функции также меняется на противоположное, т. е. у(-х) = -у(х). График нечетной функции всегда симметричен относительно начала координат.
На рисунке приведены (для наглядности) графики четной, нечетной функции и функции, не имеющей никакой четности.
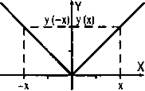
Четная функция у(-х) = у(х)
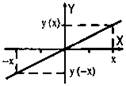
Нечетная функция у(-х) = -у(х)
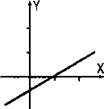
Функция, не имеющая четности
Пример 10
Выяснить четность следующих функций: ![]()
Прежде всего отметим, что область определения всех трех функций (любые х) — симметричная. Для выяснения четности этих функций у(х) остается найти значение у(-х) и сравнить значения у(х) и у(-х).
а) ![]() (здесь было учтено, что
(здесь было учтено, что ![]() ). Теперь легко видеть, что у(-х) совпадает с данной функцией у(х), т. е. у(-х) = у(х). Поэтому данная функция четная и ее график симметричен относительно оси ординат.
). Теперь легко видеть, что у(-х) совпадает с данной функцией у(х), т. е. у(-х) = у(х). Поэтому данная функция четная и ее график симметричен относительно оси ординат.

б) ![]() Видно, что значения функции в точках х и -х противоположны по знаку, т. е. у(-х) = -у(х). Поэтому данная функция нечетная и ее график симметричен относительно начала координат.
Видно, что значения функции в точках х и -х противоположны по знаку, т. е. у(-х) = -у(х). Поэтому данная функция нечетная и ее график симметричен относительно начала координат.
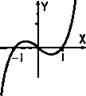
в) ![]() Сравнивая у(-х) = -2х - 4 со значением y(-х) = 2х - 4, видим, что соотношение у(-х) = y(х) не выполняется. Поэтому эта функция не будет четной. Найдем теперь величину -у(-х) = -(2х - 4) = -2х + 4. Сравнивая у(-х) = -2х - 4 и -у(х) = -2х + 4, видим, что соотношение y(-х) = -у(х) также не выполняется. Поэтому эта функция не будет нечетной.
Сравнивая у(-х) = -2х - 4 со значением y(-х) = 2х - 4, видим, что соотношение у(-х) = y(х) не выполняется. Поэтому эта функция не будет четной. Найдем теперь величину -у(-х) = -(2х - 4) = -2х + 4. Сравнивая у(-х) = -2х - 4 и -у(х) = -2х + 4, видим, что соотношение y(-х) = -у(х) также не выполняется. Поэтому эта функция не будет нечетной.
Итак, данная функция никакой четности не имеет и ее график не обладает никакой симметрией.
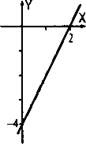
Вернемся еще раз к примеру 8. Очевидно, что функция у = 1/|x| четная (ее область определения (все х, кроме х = 0) симметрична и у(-х) = -у(х)). Поэтому график этой функции симметричен относительно оси ординат. Следовательно, достаточно построить график только для положительных значений х и симметрично отразить его относительно оси ординат в область отрицательных значений х. В итоге получается график, приведенный в примере 8.
Пример 11
Построить график функции ![]()
Область определения функции задается условием |х| - 1 ≠ 0, т. е. |х| ≠ 1 и х ≠ ± 1. Эта область является симметричной. Проверим, что данная функция четная. Найдем ![]() Видно, что выполняется соотношение у(-х) = у(х) для всех х из области определения функции. Поэтому график функции будет симметричен относительно оси ординат.
Видно, что выполняется соотношение у(-х) = у(х) для всех х из области определения функции. Поэтому график функции будет симметричен относительно оси ординат.
При х ≥ 0 по определению |х| = x и функцию можно записать в виде ![]() (при этом x ≠ 1).
(при этом x ≠ 1).
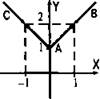
Поэтому строим график линейной функции у = х + 1 для неотрицательных значений х (луч АВ), удаляем из него точку с абсциссой х = 1 (показана стрелками). Затем этот график симметрично отражаем относительно оси ординат (получаем луч АС). Поэтому графиком данной функции является ломаная САВ.
Пример 12
Построить график функции ![]()
Аналогично предыдущему примеру устанавливаем, что область определения функции (все х, кроме х = ± 1) симметрична. Найдем ![]()
![]() Так как выполнено равенство у(-х) = -y(x), то данная функция нечетная. Поэтому ее график симметричен относительно начала координат.
Так как выполнено равенство у(-х) = -y(x), то данная функция нечетная. Поэтому ее график симметричен относительно начала координат.
Для х ≥ 0 данная функция является дробно-линейной функцией ![]() Строим график этой функции (гипербола).
Строим график этой функции (гипербола).
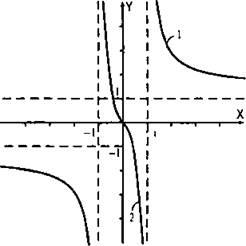
Он состоит из ветви 1 целиком и части ветви 2. Построенный график симметрично отражаем относительно начала координат. При этом асимптота х = 1 отражается в асимптоту х = -1, асимптота у = 1 отражается в асимптоту у = -1.
Итак, для построения графика функции, содержащей модуль величины, надо раскрыть этот модуль. После этого построить части графика, учитывая ограничения на переменную x. Если функция обладает определенной четностью (т. е. является четной или нечетной), то достаточно построить часть графика функции для х ≥ 0. Затем симметрично отразить эту часть графика относительно оси ординат, если функция четная, и относительно начала координат, если функция нечетная.
Более детально о функциях, их свойствах, построении графиков функций, основных преобразованиях графиков функций будет рассказано в 9 классе.
IV. Задание на уроке и дома
1. Постройте график функции:
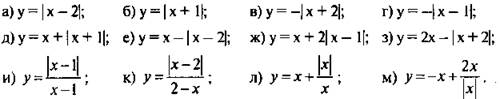
Ответы:
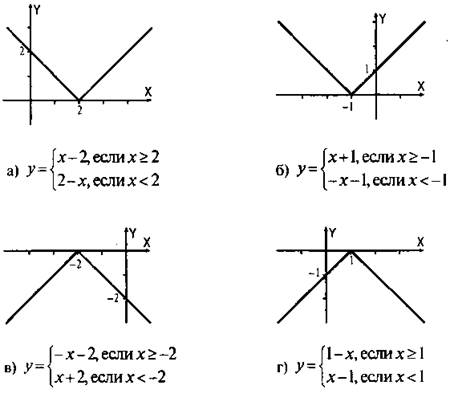
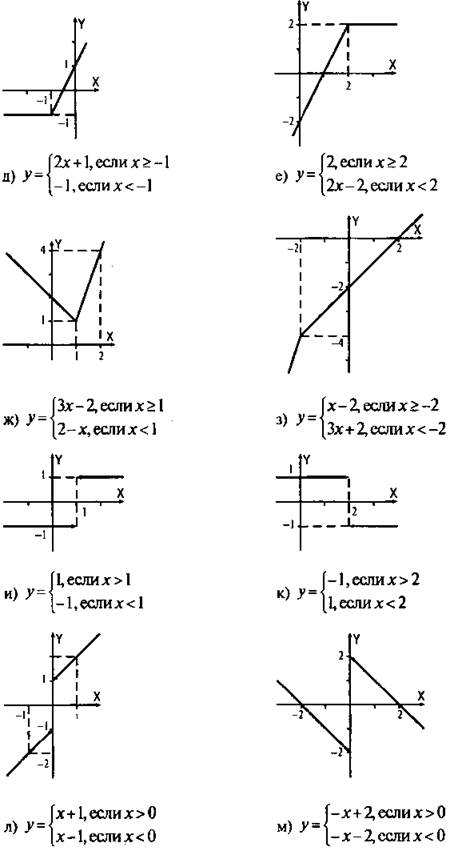
2. Постройте график функции:
![]()
Ответы:

3. Постройте график функции:
![]()
Ответы:


4. Определите четность (нечетность) функции и постройте ее график:
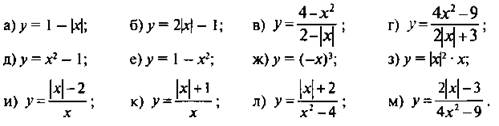
Ответы:
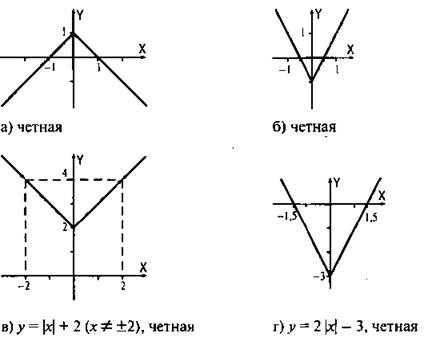
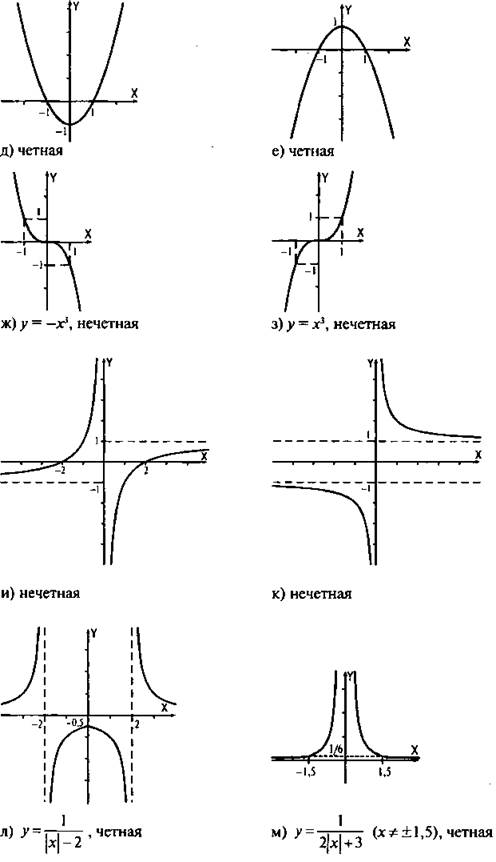
5. Определите четность (нечетность) функции и постройте ее график:
![]()
Ответы:

V. Контрольные вопросы
1. Дайте определение модуля числа.
2. Геометрический смысл модуля числа.
3. Перечислите основные свойства модуля числа.
4. Какая область определения функции называется симметричной?
5. Дайте определение:
а) четной,
б) нечетной функции.
6. Симметрия графика:
а) четной,
б) нечетной функции.
VI. Подведение итогов урока