Поурочное планирование по алгебре 7 класс
Системы линейных уравнений с двумя переменными - ІV четверть - Системы линейных уравнений
ЦЕЛЬ УРОКА: Ввести понятия системы линейных уравнений с двумя переменными, решения системы. Научить находить решения системы графическим способом.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
3 |
Устная работа |
Актуализировать опорные знания |
5 |
4 |
Изложение нового материала |
Ввести понятия системы линейных уравнений с двумя переменными, решения системы |
7 |
5 |
Тренировочные упражнения |
Научить находить решения системы графическим способом |
17 |
6 |
Упражнения на повторение |
Повторить решение уравнений, действия с многочленами |
6 |
7 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
2 |
8 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
ХОД УРОКА
I. Организационный момент
II. Проверка домашнего задания (фронтально)
III. Устная работа
1) Найти все пары натуральных чисел, которые являются решениями уравнения х + у = 11.
2) Выразить переменную у через переменную х из уравнения:
а) х + у = 4;
б) 2х - у = 2; .
в) х + 2у = 4;
г) х - у = 0.
3) При каких значениях k и b график линейной функции y = kx + b:
а) параллелен графику функции у = -6х + 8;
б) пересекает график функции у = -6х + 8;
в) совпадает с графиком функции у = -6х + 8?
IV. Изложение нового материала
1. Рассмотреть задачу на с. 194 п. 42.
2. Установить смысл термина «система уравнений» — несколько уравнений, в которых одни и те же буквы обозначают одни и те же числа. Или — несколько уравнений, для которых надо найти общие решения.
3. Привести примеры.
4. Сформулировать определение решения системы уравнений с двумя переменными.
5. Определить, что значит решить систему уравнений.
6. Чтобы показать, что данная в задаче на с. 194 система не имеет других решений, можно построить графики уравнений, составляющих систему: 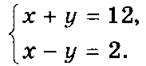
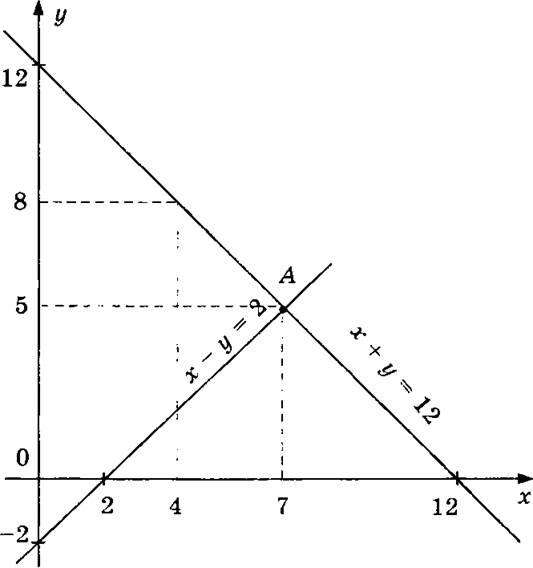
7. Правило решения системы графическим способом:
1) построить график каждого из уравнений системы;
2) найти координаты точки пересечения построенных прямых (если они пересекаются). (Пример на с. 195 рис. 78.)
8. Рассмотреть примеры 1—3 п. 42 на три возможных случая взаимного расположения двух прямых — графиков уравнений системы:
1) Прямые пересекаются, т.е. имеют одну общую точку. Тогда система уравнений имеет единственное решение (пример 1 с. 196).
2) Прямые параллельны, т.е. не имеют общих точек. Тогда система уравнений не имеет решений (пример 2 с. 196).
3) Прямые совпадают. Система уравнений имеет бесконечное множество решений (пример 3 с. 196).
V. Тренировочные упражнения
№ 1056 — устно;
№№ 1060, 1062 — на доске и в тетрадях.
Приведем здесь решение № 1062:

№ 1064 (а) — на доске и в тетрадях. Приведем его решение:
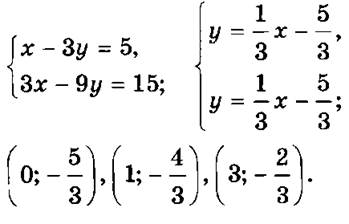
VI. Упражнения на повторение
№№ 1065 (а), 1066 (а) — самостоятельно с проверкой.
VII. Итог урока
VIII. Домашнее задание.
п. 42, №№ 1058, 1061, 1063, 1067 (а).