Разложение на множители с помощью формул квадрата суммы и квадрата разности - ІІІ четверть - Формулы сокращенного умножения

ЦЕЛЬ УРОКА: Формирование умений раскладывать многочлен на множители с помощью формул квадрата суммы и квадрата разности.

ПЛАН УРОКА:

№	Этап урока	Содержание	Время (мин)
1	Организационный момент	Нацелить учащихся на урок	1
2	Проверка домашнего задания	Коррекция ошибок	5
3	Устная работа	Актуализировать опорные знания	6
4	Изучение нового материала	Показать возможность использовать формулы (а ± b)2 для разложения многочлена на множители	5
5	Первичное закрепление материала	Формировать умение раскладывать многочлен на множители с помощью формул (а ± b)2	5
6	Тренировочные упражнения	Формировать умение раскладывать многочлен на множители с помощью формул (а ± b)2	19
7	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке	2
8	Сообщение домашнего задания	Разъяснить содержание домашнего задания	2

ХОД УРОКА

I. Организационный момент.

II. Проверка домашнего задания (фронтально).

III. Устная работа.

1) Сформулировать, как возвести в квадрат сумму двух одночленов.

2) Сформулировать, как возвести в квадрат разность двух одночленов.

3) Представить, если возможно, выражение в виде квадрата одночлена: 9а4; 4/9х6; 0,01х2y6; 36у10; 16х5.

4) Представить в виде удвоенного произведения: 12а; 16b; 2х; 4n; 10ху.

5) Заменить знак (*) таким одночленом, чтобы равенство было верным:

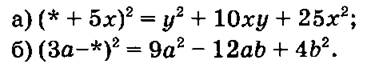
IV. Изложение нового материала.

1) По формулам сокращенного умножения имеем равенства:

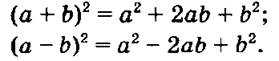
2) Перепишем эти равенства так:

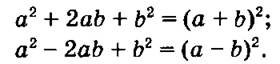
В левых частях каждого равенства — многочлены, содержащие квадрат одного члена, квадрат другого члена и удвоенное произведение этих членов.

В правых частях — их разложение на множители а + b и а + b или а - b и а - b.

Формулы сокращенного умножения дают возможность облегчить разложение многочлена на множители.

3) Примеры:

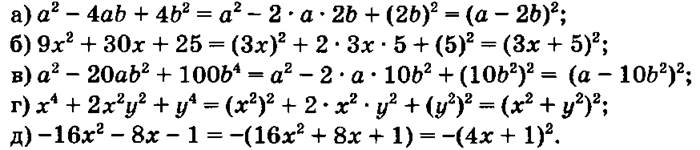
Обращаем внимание учеников на возможность проверок справа налево.

V. Первичное закрепление нового материала.

Устно:

1) Проверить справедливость равенств. Объяснить ошибку в неверно решенном примере:

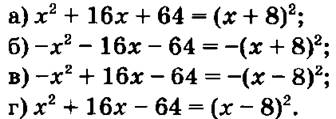
2) Разложить на множители трехчлен:

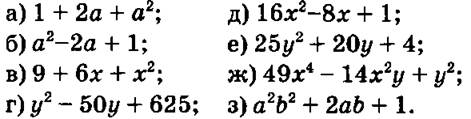
VI. Тренировочные упражнения.

№ 833 — самостоятельно с последующей проверкой.

№ 834 (а, д) — на доске и в тетрадях;

№ 834 (б, в, г, е) — самостоятельно с проверкой;

№ 836 — устно;

№№ 837, 839 — на доске и в тетрадях.

VII. Итог урока.

Привести пример трехчлена, который можно представить в виде:

а) квадрата суммы;

б) квадрата разности.

VIII. Домашнее задание.

п. 33, №№ 835,838, 977 (г, д, е), 882.