Алгебра и начала анализа для учащихся 11 класса поурочные планы
обобщение и систематизация знаний учащихся; упражнять в решении логарифмических уравнений и неравенств; подготовиться к контрольной работе - РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие
Цели: обобщение и систематизация знаний учащихся; упражнять в решении логарифмических уравнений и неравенств; подготовиться к контрольной работе.
Ход урока
I. Анализ проверочной работы
1. Указать ошибки, допущенные учащимися при выполнении работы.
2. Решить задания из домашней работы, вызвавшие затруднения у учащихся.
II. Решение логарифмических и показательных уравнений, систем М неравенств
1. Решите уравнение:
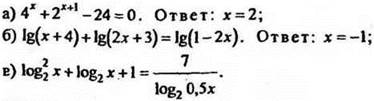
Решение
ОДЗ х > 0. Т. к. ![]() то заданное уравнение можно записать таким образом:
то заданное уравнение можно записать таким образом: 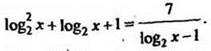
Введём новую переменную, положив ![]()
Получим ![]() и далее
и далее ![]() y3 – 1 = 7; y3 = 8; у = 2. Но у = log2 х поэтому из уравнения log2 х = 2 находим х = 4;
y3 – 1 = 7; y3 = 8; у = 2. Но у = log2 х поэтому из уравнения log2 х = 2 находим х = 4;
Ответ: х = 4.
![]()
Ответ: х = 0,2 и х = 125;
д) решить № 524 (в, г);
![]()
Решение
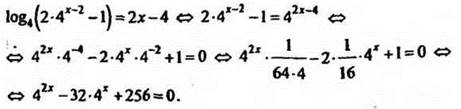
Обозначим 4х = у, где у > 0, тогда ![]() значит
значит ![]()
Проверка ![]() = верно.
= верно.
Ответ: х = 2;
![]()
Решение
![]()
Обозначим 2х = у, у > 0, тогда решим ![]() у1 = -1 не удовлетворяет условию у > 0; у2 = 4.
у1 = -1 не удовлетворяет условию у > 0; у2 = 4.
Если у = 4, то 2х = 4; 2х = 22, значит х = 2. Сделать проверку.
Ответ: х = 2.
2. Решить неравенства: .
1) № 527 (а, б); ![]()
Решение
Обозначим ![]() Решим неравенство
Решим неравенство ![]()
![]()
![]() решаем неравенство методом интервалов:
решаем неравенство методом интервалов:

Рис. 28
![]()
Ответ: [1/4;8].
![]()
Решение
Обозначим 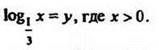
Решим неравенство ![]() методом интервалов:
методом интервалов:
![]()
Рис. 29
![]() значит,
значит, ![]() при условии х > 0.
при условии х > 0.
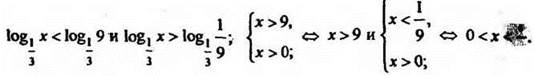
Ответ: 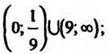
2*) решить неравенство: ![]()
Решение
Находим ОДЗ: 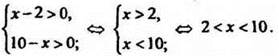
Учитывая, что основание логарифма меньше 1, решим неравенство ![]()
Т. к. х![]() (2;10), то знаменатель дроби (10 - х) при этих значениях положителен, тогда
(2;10), то знаменатель дроби (10 - х) при этих значениях положителен, тогда ![]() Учитывая, что х
Учитывая, что х![]() (2;10), окончательно имеем
(2;10), окончательно имеем 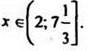 Ответ:
Ответ: 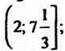
3) найти решение неравенства ![]()
Решение
Обозначим ![]() при условии
при условии 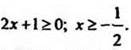
Решим неравенство ![]()

Рис. 30
Значит, < у < 5. Т. к. ![]() имеем
имеем ![]() и учитывая ОДЗ х ≥ -1/2 имеем -1/2 ≤ х < 0. Ответ [-1/2;0).
и учитывая ОДЗ х ≥ -1/2 имеем -1/2 ≤ х < 0. Ответ [-1/2;0).
3. Решить систему уравнений № 530 (б, в).
III. Итоги урока
IV. Домашнее задание: подготовиться к контрольной работе; повторить п. 35-39; решить № 524 (а; б), № 527 (в; г), № 529 (б; г). № 530 (а; г).