Алгебра и начала анализа для учащихся 11 класса поурочные планы
рассмотреть способы решения показательных неравенств и способствовать выработке навыков их решения - РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие
Цели: рассмотреть способы решения показательных неравенств и способствовать выработке навыков их решения.
Ход урока
I. Итоги математического диктанта
1. Анализ ошибок» допущенных учащимися в работе.
2. Решить на доске задания из домашней работы, вызвавшие затруднения у учащихся.
II. Изучение нового материала
1. Неравенство, содержащее переменную в показателе степени, называется показательны.
2. Решение показательных неравенств вида ![]() основано на следующих утверждениях:
основано на следующих утверждениях:
если а > 1, то неравенства ![]() равносильны;
равносильны;
если 0 < а < 1, то неравенства ![]() равносильны (это следует из того, что при а > 1 показательная функция возрастает, а при 0 < а < 1 убывает).
равносильны (это следует из того, что при а > 1 показательная функция возрастает, а при 0 < а < 1 убывает).
3. Разобрать по учебнику решение примеров 5, 6 и 7 на стр. 221 -222 с записью в тетрадях.
III. Решение показательных неравенств
1. Решить № 466 (б; г) и № 467 (б; г).
2. Решить № 473 (а; б)
![]()
Решение
Обозначим 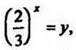 где у > 0, тогда имеем
где у > 0, тогда имеем 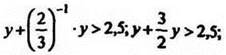
![]() Значит,
Значит, ![]() Поскольку
Поскольку ![]() то х < 0. Ответ: (-∞;0);
то х < 0. Ответ: (-∞;0);
![]()
Решение
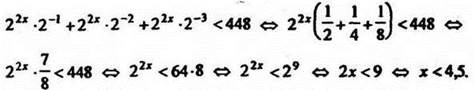
Ответ: (-∞;4,5).
3. Решить № 474 (а; б):
а) решить неравенство ![]()
Решение
Обозначим ![]() х = у, где у > 0. Искомое неравенство примет вид
х = у, где у > 0. Искомое неравенство примет вид ![]() которое решим методом интервалов:
которое решим методом интервалов: ![]() Нули функции
Нули функции ![]() равны у1 = 0, у2 = 1.
равны у1 = 0, у2 = 1.

Рис. 22
Решение неравенства 0 < у ≤ 1. Так как ![]() ≈ 3,14 > 1, то
≈ 3,14 > 1, то ![]() Ответ: (-∞;0];
Ответ: (-∞;0];
б) решить неравенство (самостоятельно): ![]()
Указание.
Преобразуем ![]()
Обозначим ![]() тогда неравенство примет вид
тогда неравенство примет вид ![]()
4*. Найти наименьшее целое х, удовлетворяющее неравенству ![]()
Решение
Соберём все степени с основанием 2 в одну часть неравенства, а степени с основанием 11 -в другую:
![]()
Разделим обе части неравенства на ![]()
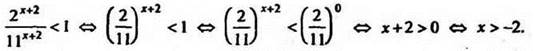
Наименьшее целое х из этого промежутка х = -1. Ответ: х = -1.
5*. Найти наибольшее целое х, удовлетворяющее неравенству ![]()
Решение
Обозначим ![]() Исходное неравенство примет вид
Исходное неравенство примет вид ![]() Умножим обе части неравенства на у (при этом смысл неравенства не изменится, т. к. у > 0 по определению).
Умножим обе части неравенства на у (при этом смысл неравенства не изменится, т. к. у > 0 по определению).
Получим 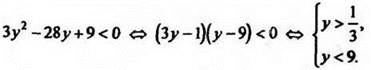
Переходя от у к искомой функции ![]() имеем
имеем
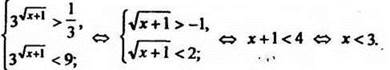
Учитывая область допустимых значений исходного неравенства (х > - 1), имеем х![]() (-1;3). Наибольшее целое х из этого промежутка х = 2.
(-1;3). Наибольшее целое х из этого промежутка х = 2.
Ответ: 2.
IV. Итоги урока
V. Домашнее задание: подготовиться к письменному зачёту, повторив материал п. 35 и п. 36; решить № 471, На 472, № 473 (в; г), № 474 (в; г).